Boundary parallel
In mathematics, a closed n-manifold N embedded in an (n + 1)-manifold M is boundary parallel (or ∂-parallel, or peripheral) if there is an isotopy of N onto a boundary component of M. (Wikipedia).

In mathematics, a closed n-manifold N embedded in an (n + 1)-manifold M is boundary parallel (or ∂-parallel, or peripheral) if there is an isotopy of N onto a boundary component of M. (Wikipedia).


What are parallel lines and a transversal
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal
What are the Angle Relationships for Parallel Lines and a Transversal
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal
Proving Parallel Lines with Angle Relationships
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal
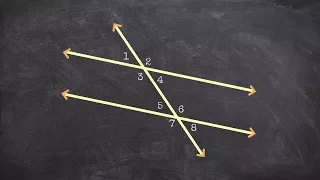
How To Determine If Two Lines are Parallel to Apply Angle Theorems
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal

Corresponding Angles Theorem with Parallel Lines
👉 Learn about parallel lines and a transversal theorems. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated in both lines
From playlist Parallel Lines and a Transversal Theorems
What is the Consecutive Interior Angle Converse Theorem
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal

What is the Corresponding Angle Converse Theorem
👉 Learn about converse theorems of parallel lines and a transversal. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated i
From playlist Parallel Lines and a Transversal

Consecutive Angles Theorem with Parallel Lines
👉 Learn about parallel lines and a transversal theorems. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated in both lines
From playlist Parallel Lines and a Transversal Theorems

Rod Gover - Geometric Compactification, Cartan holonomy, and asymptotics
Conformal compactification has long been recognised as an effective geometric framework for relating conformal geometry, and associated field theories « at infinity », to the asymptotic phenomena of an interior (pseudo‐)‐Riemannian geometry of one higher dimension. It provides an effective
From playlist Ecole d'été 2014 - Analyse asymptotique en relativité générale

Fresnel Equations Part 2: Deriving the Equations
The Fresnel Equations Part 3 of a series on electromagnetic radiation: The Fresnel Equations - deriving from Maxwell's equations the boundary conditions when EM radiation passes between two dielectrics and deriving the Fresnel equations which describe the proportion of the E vector which i
From playlist Electricity & Magnetism

Joel Hass - Lecture 3 - Algorithms and complexity in the theory of knots and manifolds - 20/06/18
School on Low-Dimensional Geometry and Topology: Discrete and Algorithmic Aspects (http://geomschool2018.univ-mlv.fr/) Joel Hass (University of California at Davis, USA) Algorithms and complexity in the theory of knots and manifolds Abstract: These lectures will introduce algorithmic pro
From playlist Joel Hass - School on Low-Dimensional Geometry and Topology: Discrete and Algorithmic Aspects

What is an example of lines that are a linear pair
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

Known Boundary Emulation of Complex Computer Models: Ian Vernon, Cambridge
Uncertainty quantification (UQ) employs theoretical, numerical and computational tools to characterise uncertainty. It is increasingly becoming a relevant tool to gain a better understanding of physical systems and to make better decisions under uncertainty. Realistic physical systems are
From playlist Effective and efficient gaussian processes

الاهتزازات والأمواج (جامعة إم آي تي) - المحاضرة 18: الشروط الحدِّية للعوازل
MIT المحاضرة الثامنة عشرة من مساق "الاهتزازات والأمواج" من جامعة إم آي تي للبروفيسور والتر لوين وهي عن الشروط الحدِّية للعوازل بالإضافة للفيديو هناك ملفات مرفقة على موقعنا الالكتروني: https://shamsunalarabia.net/courses/الاهتزازات-والأمواج/ رابط المساق https://www.youtube.com/watch?v=Ff
From playlist 8.03 Arabic Subtitles
Rod Gover - An introduction to conformal geometry and tractor calculus (Part 3)
After recalling some features (and the value of) the invariant « Ricci calculus » of pseudo‐Riemannian geometry, we look at conformal rescaling from an elementary perspective. The idea of conformal covariance is visited and some covariant/invariant equations from physics are recovered in
From playlist Ecole d'été 2014 - Analyse asymptotique en relativité générale

Mod-01 Lec-14 Finite Difference Method (contd.) and Polynomial Interpolations
Advanced Numerical Analysis by Prof. Sachin C. Patwardhan,Department of Chemical Engineering,IIT Bombay.For more details on NPTEL visit http://nptel.ac.in
From playlist IIT Bombay: Advanced Numerical Analysis | CosmoLearning.org
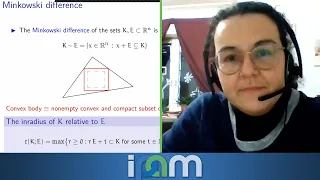
Eugenia Saorin-Gomez - Inner parallel bodies & the Isoperimetric Quotient
Recorded 10 February 2022. Eugenia Saorin-Gomez of the Universität Bremen presents "Inner parallel bodies & the Isoperimetric Quotient" at IPAM's Calculus of Variations in Probability and Geometry Workshop. Abstract: The so-called Minkowski difference of convex bodies (compact and convex s
From playlist Workshop: Calculus of Variations in Probability and Geometry

Learn how to use Snell's Law to analyze complex refraction scenarios. Four example problems are solved. The Snell's Law of Refraction Video Tutorial (referenced on Slide 3) can be found at: https://youtu.be/PUUQk7VPPfQ You can find more information that supports this video on our websi
From playlist Refraction and Lenses

Tobias Colding (MIT): 1/3 Geometric heat equations [Coxeter Lecture Series 2017]
Geometric heat equations Speaker: Tobias Colding, Massachusetts Institute of Technology Date and Time: Wednesday, November 15, 2017 - 3:30pm to 4:30pm Location: Fields Institute, Room 230 Abstract: The classical heat equation describes how a temperature distribution changes in time. Ov
From playlist Mathematics

👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships