
Présentation de l'exposition "Emile Borel : un mathématicien au pluriel"
---------------------------------- Institut Henri Poincaré, 11 rue Pierre et Marie Curie, 75005 PARIS http://www.ihp.fr/ Rejoignez les réseaux sociaux de l'IHP pour être au courant de nos actualités : - Facebook : https://www.facebook.com/InstitutHenriPoincare/ - Twitter : https://twitter
From playlist Bibliothèque

This lecture is part of an online course on rings and modules. We continue the previous lecture on complete rings by discussing Hensel's lemma for finding roots of polynomials over p-adic rings or over power series rings. We sketch two proofs, by slowly improving a root one digit at a tim
From playlist Rings and modules

Emile Borel: Real number enthusiast or skeptic? | Sociology and Pure Mathematics | N J Wildberger
Emile Borel was a prominent French analyst and probabilist, and the founder of modern measure theory. He was also involved in the issue of "real numbers" and just what they actually are, and what it means to do arithmetic with them. This is a first introduction to his thinking, where we d
From playlist Sociology and Pure Mathematics

Here I prove the Heine-Borel Theorem, one of the most fundamental theorems in analysis. It says that in R^n, all boxes must be compact. The proof itself is very neat, and uses a bisection-type argument. Enjoy! Topology Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmA13vj9xkHG
From playlist Topology

CurvesSurfaces3: De Casteljau Bezier Curves in Algebraic Calculus | N J Wildberger
We explain how to extend Archimedes' famous Parabolic Area Formula to the cubic situation. This formula was historically the first major calculation in Calculus, and gave an explicit and workable formula for the area of a slice of a parabola, cut off by a chord, in terms of the area of a p
From playlist MathSeminars

This course is on Lemma: http://lem.ma Lemma looking for developers: http://lem.ma/jobs Other than http://lem.ma, I recommend Strang http://bit.ly/StrangYT, Gelfand http://bit.ly/GelfandYT, and my short book of essays http://bit.ly/HALAYT Questions and comments below will be prompt
From playlist Problems, Paradoxes, and Sophisms

Natasha Dobrinen: Borel sets of Rado graphs are Ramsey
The Galvin-Prikry theorem states that Borel partitions of the Baire space are Ramsey. Thus, given any Borel subset $\chi$ of the Baire space and an infinite set $N$, there is an infinite subset $M$ of $N$ such that $\left [M \right ]^{\omega }$ is either contained in $\chi$ or disjoint fr
From playlist Combinatorics

Borel-Cantelli Lemmas for Inhomogeneous Diophantine Approximations and beyond by Victor Beresnevich
PROGRAM : ERGODIC THEORY AND DYNAMICAL SYSTEMS (HYBRID) ORGANIZERS : C. S. Aravinda (TIFR-CAM, Bengaluru), Anish Ghosh (TIFR, Mumbai) and Riddhi Shah (JNU, New Delhi) DATE : 05 December 2022 to 16 December 2022 VENUE : Ramanujan Lecture Hall and Online The programme will have an emphasis
From playlist Ergodic Theory and Dynamical Systems 2022
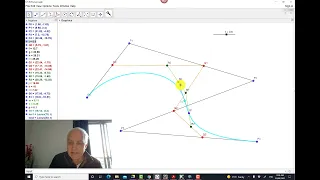
Polynumbers and de Casteljau Bezier curves | Algebraic Calculus and dCB curves | N J Wildberger
The Algebraic Calculus is an exciting new approach to calculus, not reliant on "infinite processes" and "real numbers". The central objects are polynomially parametrized curve, which turn out to be the same as the de Casteljau Bezier curves which play such a big role in design, animation,
From playlist Algebraic Calculus One Info

The role of topology and compactness (...) - CEB T2 2017 - Varadhan - 3/3
S.R.S. Varadhan (Courant Institute) - 09/06/2017 The role of topology and compactness in the theory of large deviations When a large deviation result is proved there is some topology involved in the statement because it affects the class of sets for which the estimates hold. Often the cho
From playlist 2017 - T2 - Stochastic Dynamics out of Equilibrium - CEB Trimester

This course is on Lemma: http://lem.ma Lemma looking for developers: http://lem.ma/jobs Other than http://lem.ma, I recommend Strang http://bit.ly/StrangYT, Gelfand http://bit.ly/GelfandYT, and my short book of essays http://bit.ly/HALAYT Questions and comments below will be prompt
From playlist Problems, Paradoxes, and Sophisms

Eulalia Nualart: Asymptotics for some non-linear stochastic heat equations
Abstract: Consider the following stochastic heat equation, ∂ut(x)/∂t = −ν(−Δ)α/2ut(x)+σ(ut(x))F˙(t,x),t[is greater than]0,x∈ℝd. Here −ν(−Δ)α/2 is the fractional Laplacian with ν[is greater than]0 and α∈(0,2], σ:ℝ→ℝ is a globally Lipschitz function, and F˙(t,x) is a Gaussian noise which is
From playlist Probability and Statistics

Proof of Lemma and Lagrange's Theorem
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Proof of Lemma and Lagrange's Theorem. This video starts by proving that any two right cosets have the same cardinality. Then we prove Lagrange's Theorem which says that if H is a subgroup of a finite group G then the order of H div
From playlist Abstract Algebra

Rolf Schneider: Hyperplane tessellations in Euclidean and spherical spaces
Abstract: Random mosaics generated by stationary Poisson hyperplane processes in Euclidean space are a much studied object of Stochastic Geometry, and their typical cells or zero cells belong to the most prominent models of random polytopes. After a brief review, we turn to analogues in sp
From playlist Probability and Statistics

An explicit supercuspidal local Langlands correspondence - Tasho Kaletha
Joint IAS/Princeton University Number Theory Seminar Topic: An explicit supercuspidal local Langlands correspondence Speaker: Tasho Kaletha Affiliation: University of Michigan; von Neumann Fellow, School of Mathematics Date: October 29, 2020 For more video please visit http://video.ias.e
From playlist Mathematics

Here I give an interesting example of a set that is closed and bounded, but not compact. So in some sense this is an infinite-dimensional counterexample to the Heine-Borel theorem. Heine-Borel Theorem: https://youtu.be/4jaox_jqwGM Topology Playlist: https://www.youtube.com/playlist?list=P
From playlist Topology

Kęstutis Česnavičius - Grothendieck–Serre in the quasi-split unramified case
Correction: The affiliation of Lei Fu is Tsinghua University. The Grothendieck–Serre conjecture predicts that every generically trivial torsor under a reductive group scheme G over a regular local ring R is trivial. We settle it in the case when G is quasi-split and R is unramified. To ov
From playlist Conférence « Géométrie arithmétique en l’honneur de Luc Illusie » - 5 mai 2021

Math 131 Fall 2018 100318 Heine Borel Theorem
Definition of limit point compactness. Compact implies limit point compact. A nested sequence of closed intervals has a nonempty intersection. k-cells are compact. Heine-Borel Theorem: in Euclidean space, compactness, limit point compactness, and being closed and bounded are equivalent
From playlist Course 7: (Rudin's) Principles of Mathematical Analysis (Fall 2018)

