
What is the Riemann Hypothesis?
This video provides a basic introduction to the Riemann Hypothesis based on the the superb book 'Prime Obsession' by John Derbyshire. Along the way I look at convergent and divergent series, Euler's famous solution to the Basel problem, and the Riemann-Zeta function. Analytic continuation
From playlist Mathematics
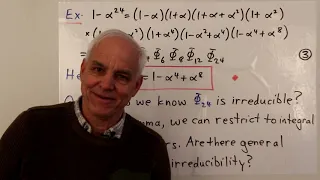
Irreducibility and the Schoenemann-Eisenstein criterion | Famous Math Probs 20b | N J Wildberger
In the context of defining and computing the cyclotomic polynumbers (or polynomials), we consider irreducibility. Gauss's lemma connects irreducibility over the integers to irreducibility over the rational numbers. Then we describe T. Schoenemann's irreducibility criterion, which uses some
From playlist Famous Math Problems

Ulrich Berger: On the Computational content of Brouwer's Theorem
The lecture was held within the framework of the Hausdorff Trimester Program: Constructive Mathematics. Abstract: The usual formulation of Brouwer's Theorem ('every bar is inductive')involves quantification over infinite sequences of natural numbers. We propose an alternative formulation
From playlist Workshop: "Constructive Mathematics"

The Dangerous Chemicals In Your Plastic Packages
Plastic is everywhere. In grocery receipts, water bottles, and of course, food packaging. And that means that chemicals in plastic like BPA and phthalates are everywhere too. Researchers are concerned that these chemicals can leach into food and get into your body, which might have serious
From playlist Health Science

Alexander Rolle (8/12/22): Homology inference for the degree-Rips bifiltration
The degree-Rips bifiltration is a density-sensitive construction based on the Vietoris-Rips filtration. I will motivate the "degree" part of the construction, and present a framework for studying homology inference questions. I will also present an example, motivated by experiments in a re
From playlist Vietoris-Rips Seminar

Divergence Theorem. In this video, I give an example of the divergence theorem, also known as the Gauss-Green theorem, which helps us simplify surface integrals tremendously. It's, in my opinion, the most important theorem in multivariable calculus. It is also extremely useful in physics,
From playlist Vector Calculus

Supersection, More Comfortable
From playlist CS50 Sections 2015

PreCalculus - Logarithmic Function (1 of 23) What is an Logarithmic Function?
Visit http://ilectureonline.com for more math and science lectures! In this video I will define and give examples of logarithmic functions. Next video can be seen at: http://youtu.be/uLRiUMyDf64
From playlist Michel van Biezen: PRECALCULUS 1-5 - ALGEBRA REVIEW
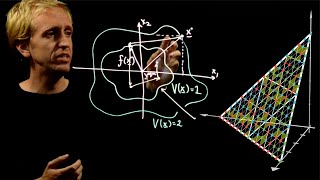
Lyapunov Stability via Sperner's Lemma
We go on whistle stop tour of one of the most fundamental tools from control theory: the Lyapunov function. But with a twist from combinatorics and topology. For more on Sperner's Lemma, including a simple derivation, please see the following wonderful video, which was my main source of i
From playlist Summer of Math Exposition Youtube Videos

Introduction to additive combinatorics lecture 10.8 --- A weak form of Freiman's theorem
In this short video I explain how the proof of Freiman's theorem for subsets of Z differs from the proof given earlier for subsets of F_p^N. The answer is not very much: the main differences are due to the fact that cyclic groups of prime order do not have lots of subgroups, so one has to
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)
Ralph Blumberg: "Design of Permanent Magnets-Based Passive Levitation Skis"
LoopTransPort 2018 Conference (with Hyperloop Advanced Research Partnership) "Design of Permanent Magnets-Based Passive Levitation Skis" Ralph Blumberg (presenter), M. Laliberte, A. Khan, A. Kunze, K. Stormo, rLoop, Inc. Abstract: In this paper we detail the design of a unique passive le
From playlist LoopTransPort 2018 Conference
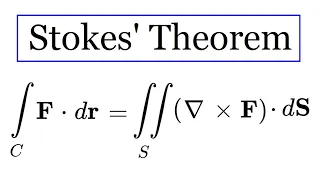
In this video, I present another example of Stokes theorem, this time using it to calculate the line integral of a vector field. It is a very useful theorem that arises a lot in physics, for example in Maxwell's equations. Other Stokes Example: https://youtu.be/-fYbBSiqvUw Yet another Sto
From playlist Vector Calculus

This lecture is part of an online course on Galois theory. This is an introductory lecture, giving an informal overview of Galois theory. We discuss some historical examples of problems that it was used to solve, such as the Abel-Ruffini theorem that degree 5 polynomials cannot in genera
From playlist Galois theory

Complex cobordism and Hamiltonian fibrations - Mohammed Abouzaid
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Complex cobordism and Hamiltonian fibrations Speaker: Mohammed Abouzaid Affiliation: Columbia University Date: November 26, 2021 I will discuss joint work with McLean and Smith, lifting the results of Seidel,
From playlist Mathematics

Michael Lesnick (2/23/2022): Stability of 2-Parameter Persistent Homology
We show that the standard stability results for union-of-balls, Čech, and Rips persistent homology have natural analogues in the 2-parameter setting, formulated in terms of the multicover bifiltration and Sheehy's subdivision bifiltrations. Our results imply that these bifiltrations are r
From playlist AATRN 2022

Michael Mandell: The strong Kunneth theorem for topological periodic cyclic homology
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Hesselholt has recently been advertising "topological periodic cyclic homology" (TP) as potentially filling some of the same roles for finite primes as periodic cyclic homology plays
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Stopping Oil Spill Pollution with Maths
Following the Deepwater Horizon oil spill in 2010, scientists at the University of Cambridge have been studying underwater plumes to try to understand how the Earth's rotation affects the spread of oil. Their experiments revealed the important role played by conservation of angular momentu
From playlist Fluid Dynamics

Thomas Nikolaus : Equivariant homotopy theory for infinite groups and THH with coefficients
CONFERENCE Recording during the thematic meeting : « Chromatic Homotopy, K-Theory and Functors» the January 24, 2023 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Jean Petit Find this video and other talks given by worldwide mathematicians on CIR
From playlist Topology

Free ebook http://tinyurl.com/EngMath A short tutorial on how to apply Gauss' Divergence Theorem, which is one of the fundamental results of vector calculus. The theorem is stated and we apply it to a simple example.
From playlist Several Variable Calculus / Vector Calculus

Ling Zhou (1/21/22): Persistent homotopy groups of metric spaces
In this talk, I will quickly overview previous work on discrete homotopy groups by Plaut et al. and Barcelo et al., and work blending homotopy groups with persistence, including those by Frosini and Mulazzani, Letscher, Jardine, Blumberg and Lesnick, and by Bantan et al. By capturing both
From playlist Vietoris-Rips Seminar