
Condense a logarithmic expression with product and quotient
👉 Learn how to condense logarithmic expressions. A logarithmic expression is an expression having logarithms in it. To condense logarithmic expressions means to use the logarithm laws to reduce logarithm expressions from the expanded form to a condensed form. Knowledge of the logarithm law
From playlist Condense Logarithms | Hard

Regularity methods in combinatorics, number theory, and computer science - Jacob Fox
Marston Morse Lectures Topic: Regularity methods in combinatorics, number theory, and computer science Speaker: Jacob Fox Affiliation: Stanford University Date: October 24, 2016 For more videos, visit http://video.ias.edu
From playlist Mathematics

13. Sparse regularity and the Green-Tao theorem
MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019 Instructor: Yufei Zhao View the complete course: https://ocw.mit.edu/18-217F19 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP62qauV_CpT1zKaGG_Vj5igX After discussion of Ramanujan graphs, Prof. Zhao discusse
From playlist MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019

Closure of VP under taking factors (Lecture - 01) by Mrinal Kumar
Discussion Meeting Workshop on Algebraic Complexity Theory  ORGANIZERS Prahladh Harsha, Ramprasad Saptharishi and Srikanth Srinivasan DATE & TIME 25 March 2019 to 29 March 2019 VENUE Madhava Lecture Hall, ICTS Bangalore Algebraic complexity aims at understanding the computationa
From playlist Workshop on Algebraic Complexity Theory 2019

A Regularity Lemma with Modifications - Guy Moshkovitz
Computer Science/Discrete Mathematics Seminar II Topic: A Regularity Lemma with Modifications Speaker: Guy Moshkovitz Affiliation: Member, School of Mathematics Date: January 29, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

24. Structure of set addition IV: proof of Freiman's theorem
MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019 Instructor: Yufei Zhao View the complete course: https://ocw.mit.edu/18-217F19 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP62qauV_CpT1zKaGG_Vj5igX This lecture concludes the proof of Freiman's theorem on
From playlist MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019

Non-commutative rank - Visu Makam
Computer Science/Discrete Mathematics Seminar II Topic: Non-commutative rank Speaker: Visu Makam Affiliation: University of Michigan; Member, School of Mathematics Date: February 5, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

Condensing logarithmic expressions
👉 Learn how to condense logarithmic expressions. A logarithmic expression is an expression having logarithms in it. To condense logarithmic expressions means to use the logarithm laws to reduce logarithm expressions from the expanded form to a condensed form. Knowledge of the logarithm law
From playlist Condense Logarithms | Hard

Condensing logarithmic expressions
👉 Learn how to condense logarithmic expressions. A logarithmic expression is an expression having logarithms in it. To condense logarithmic expressions means to use the logarithm laws to reduce logarithm expressions from the expanded form to a condensed form. Knowledge of the logarithm law
From playlist Condense Logarithms | Hard

Condensing logarithmic expressions
👉 Learn how to condense logarithmic expressions. A logarithmic expression is an expression having logarithms in it. To condense logarithmic expressions means to use the logarithm laws to reduce logarithm expressions from the expanded form to a condensed form. Knowledge of the logarithm law
From playlist Condense Logarithms | Hard
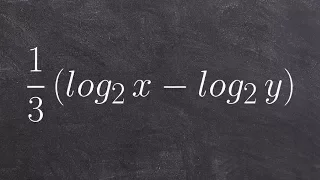
How to condense a logarithmic expression using a radical
👉 Learn how to condense logarithmic expressions. A logarithmic expression is an expression having logarithms in it. To condense logarithmic expressions means to use the logarithm laws to reduce logarithm expressions from the expanded form to a condensed form. Knowledge of the logarithm law
From playlist Condense Logarithms with Brackets

The MAIN LEMMA, Lefschetz pencils, sketch of proof of RH, beginning of proof of Main Lemma
From playlist Étale cohomology and the Weil conjectures

[Lesson 27.5 optional] QED Prerequisites Scattering 4.5 An application of Cauchy's Theorem
THis is a supplemental lecture to Scattering 4. In this lesson we practice using complex contour integration to evaluate one of the standard integrals used in the development of the formula of stationary phase. This lesson exercises the use of Cauchy's Theorem and Jordan's Lemma. Note: th
From playlist QED- Prerequisite Topics

Some closure results for polynomial factorization - Mrinal Kumar
Computer Science/Discrete Mathematics Seminar II Topic: Some closure results for polynomial factorization Speaker: Mrinal Kumar Affiliation: Harvard University Date: Febuary 20, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Negative Self Intersection Example
A lot of people say they have trouble with this so I decided to make a video on it.
From playlist One-off Explanations

Condensing logarithmic expressions
👉 Learn how to condense logarithmic expressions. A logarithmic expression is an expression having logarithms in it. To condense logarithmic expressions means to use the logarithm laws to reduce logarithm expressions from the expanded form to a condensed form. Knowledge of the logarithm law
From playlist Condense and Expand Logarithms

Condensing logarithmic expressions
👉 Learn how to condense logarithmic expressions. A logarithmic expression is an expression having logarithms in it. To condense logarithmic expressions means to use the logarithm laws to reduce logarithm expressions from the expanded form to a condensed form. Knowledge of the logarithm law
From playlist Condense and Expand Logarithms

Condensing logarithmic expressions
👉 Learn how to condense logarithmic expressions. A logarithmic expression is an expression having logarithms in it. To condense logarithmic expressions means to use the logarithm laws to reduce logarithm expressions from the expanded form to a condensed form. Knowledge of the logarithm law
From playlist Condense and Expand Logarithms
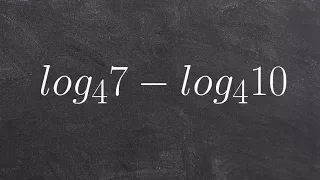
Condensing logarithmic expressions
👉 Learn how to condense logarithmic expressions. A logarithmic expression is an expression having logarithms in it. To condense logarithmic expressions means to use the logarithm laws to reduce logarithm expressions from the expanded form to a condensed form. Knowledge of the logarithm law
From playlist Condense and Expand Logarithms

Condensing logarithmic expressions
👉 Learn how to condense logarithmic expressions. A logarithmic expression is an expression having logarithms in it. To condense logarithmic expressions means to use the logarithm laws to reduce logarithm expressions from the expanded form to a condensed form. Knowledge of the logarithm law
From playlist Condense and Expand Logarithms