
The Axiom of Choice | Epic Math Time
The axiom of choice states that the cartesian product of nonempty sets is nonempty. This doesn't sound controversial, and it might not even sound interesting, but adopting the axiom of choice has far reaching consequences in mathematics, and applying it in proofs has a very distinctive qua
From playlist Latest Uploads

Axiomatics and the least upper bound property (I) | Real numbers and limits Math Foundations 120
The role of axiomatics in mathematics is a highly contentious one. Originally the term always referred to Euclid, and his use of the term to mean `a self-evident truth that requires no proof '. However in modern times the meaning of the term has shifted dramatically, to the idea that an Ax
From playlist Math Foundations

A02 Independence of the solution set
The independence of a linear system. How to make sure that a set of solutions are not constant multiples of each other.
From playlist A Second Course in Differential Equations

The Simplest Math No One Can Agree on- A Paradox of Choice
To build our mathematics we need a starting point, rules to dictate what we can do and assumed basic truths to serve as a foundation as we seek understanding of higher level problems. But what happens when we can't agree on what we should start with?
From playlist Summer of Math Exposition Youtube Videos
Equivalence relations -- Proofs
This lecture is on Introduction to Higher Mathematics (Proofs). For more see http://calculus123.com.
From playlist Proofs

What's so wrong with the Axiom of Choice ?
One of the Zermelo- Fraenkel axioms, called axiom of choice, is remarkably controversial. It links to linear algebra and several paradoxes- find out what is so strange about it ! (00:22) - Math objects as sets (00:54) - What axioms we use ? (01:30) - Understanding axiom of choice (03:2
From playlist Something you did not know...
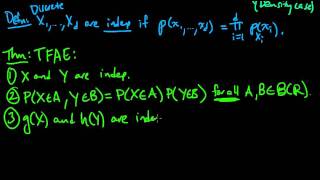
(PP 5.4) Independence, Covariance, and Correlation
(0:00) Definition of independent random variables. (5:10) Characterizations of independence. (10:54) Definition of covariance. (13:10) Definition of correlation. A playlist of the Probability Primer series is available here: http://www.youtube.com/view_play_list?p=17567A1A3F5DB5E4
From playlist Probability Theory

Relations and Functions | Axiomatic Set Theory, Section 2.1
In this video we define and prove a few basic theorems about relations and functions. My Twitter: https://twitter.com/KristapsBalodi3 Intro:(0:00) Ordered Pairs:(1:43) IMAGE-in that!:(3:33) Composition: (7:57) Functions:(11:05) Special thanks to Alex Stephens
From playlist Axiomatic Set Theory

Nonlinear algebra, Lecture 13: "Polytopes and Matroids ", by Mateusz Michalek
This is the thirteenth lecture in the IMPRS Ringvorlesung, the advanced graduate course at the Max Planck Institute for Mathematics in the Sciences.
From playlist IMPRS Ringvorlesung - Introduction to Nonlinear Algebra

Infinite Sets and Foundations (Joel David Hamkins) | Ep. 17
Joel David Hamkins is a Professor of Logic with appointments in Philosophy and Mathematics at Oxford University. His main interest is in set theory. We discuss the field of set theory: what it can say about infinite sets and which issues are unresolved, and the relation of set theory to ph
From playlist Daniel Rubin Show, Full episodes

IMS Public Lecture - Can Every Mathematical Problem Be Solved?
Menachem Magidor, The Hebrew University of Jerusalem, Israel
From playlist Public Lectures

Wolfram Physics Project: Working Session Saturday, July 25, 2020 [Metamathematics | Part 2]
This is a Wolfram Physics Project progress update at the Wolfram Summer School. This is a continuation of part two found here: https://youtu.be/x5v3KFFWv2o Originally livestreamed at: https://twitch.tv/stephen_wolfram Stay up-to-date on this project by visiting our website: http://wolfr.
From playlist Wolfram Physics Project Livestream Archive

The perfect number of axioms | Axiomatic Set Theory, Section 1.1
In this video we introduce 6 of the axioms of ZFC set theory. My Twitter: https://twitter.com/KristapsBalodi3 Intro: (0:00) The Axiom of Existence: (2:39) The Axiom of Extensionality: (4:20) The Axiom Schema of Comprehension: (6:15) The Axiom of Pair (12:16) The Axiom of Union (15:15) T
From playlist Axiomatic Set Theory

Topics in Combinatorics lecture 8.9 --- Further properties of entropy
This follows on from lecture 8.4, where I introduced the axioms for entropy. Here I talk about some further simple properties of entropy and how they follow from the axioms, using the continuity and maximization axioms for the first time. 0:00 Introduction and recap of the axioms 4:01 The
From playlist Topics in Combinatorics (Cambridge Part III course)

This is part of a series of lectures on the Zermelo-Fraenkel axioms for set theory. We dicuss the axiom of chice, and sketch why it is independent of the other axioms of set theory. For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj52EKVgPi-p50f
From playlist Zermelo Fraenkel axioms

Wolfram Physics Project: Working Session Thursday, July 23, 2020 [Metamathematics | Part 1]
This is a Wolfram Physics Project progress update at the Wolfram Summer School. Originally livestreamed at: https://twitch.tv/stephen_wolfram Stay up-to-date on this project by visiting our website: http://wolfr.am/physics Check out the announcement post: http://wolfr.am/physics-announce
From playlist Wolfram Physics Project Livestream Archive

Topics in Combinatorics lecture 8.4 --- Entropy axioms and some simple consequences
This is an introduction to the concept of entropy (in the information-theoretic sense of the word). In the next few videos I shall say more about the concept and give a few non-obvious applications of entropy to combinatorial problems. 0:00 Introduction and entropy axioms 15:17 A few simp
From playlist Topics in Combinatorics (Cambridge Part III course)

Wolfram Physics Project: Working Session Tuesday, July 28, 2020 [Metamathematics | Part 3]
This is a Wolfram Physics Project progress update at the Wolfram Summer School. This is a continuation of part two found here: https://youtu.be/ndtLa0BhEdg Originally livestreamed at: https://twitch.tv/stephen_wolfram Stay up-to-date on this project by visiting our website: http://wolfr.
From playlist Wolfram Physics Project Livestream Archive

1. Introduction and Probability Review
MIT 6.262 Discrete Stochastic Processes, Spring 2011 View the complete course: http://ocw.mit.edu/6-262S11 Instructor: Robert Gallager License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.262 Discrete Stochastic Processes, Spring 2011

Operations on Sets | Axiomatic Set Theory, Section 1.2
We define some basic operations on sets using the axioms of ZFC. My Twitter: https://twitter.com/KristapsBalodi3 Intersection:(0:00) Ordered Tuples/Products:(4:45)
From playlist Axiomatic Set Theory