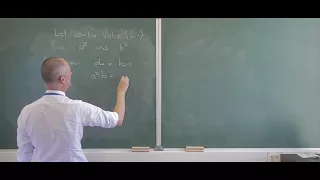Minimal surfaces | Differential geometry
Associate family
In differential geometry, the associate family (or Bonnet family) of a minimal surface is a one-parameter family of minimal surfaces which share the same Weierstrass data. That is, if the surface has the representation the family is described by where indicates the real part of a complex number. For θ = π/2 the surface is called the conjugate of the θ = 0 surface. The transformation can be viewed as locally rotating the principal curvature directions. The surface normals of a point with a fixed ζ remains unchanged as θ changes; the point itself moves along an ellipse. Some examples of associate surface families are: the catenoid and helicoid family, the Schwarz P, Schwarz D and gyroid family, and the Scherk's first and second surface family. The Enneper surface is conjugate to itself: it is left invariant as θ changes. Conjugate surfaces have the property that any straight line on a surface maps to a planar geodesic on its conjugate surface and vice versa. If a patch of one surface is bounded by a straight line, then the conjugate patch is bounded by a planar symmetry line. This is useful for constructing minimal surfaces by going to the conjugate space: being bound by planes is equivalent to being bound by a polygon. There are counterparts to the associate families of minimal surfaces in higher-dimensional spaces and manifolds. (Wikipedia).