
This levitron manufactured by my friend İzzet Özgöçmen. We enjoyed playing with it.
From playlist Izzet Özgöçmen

Cork: Is this nature's most versatile material? – BBC REEL
As well as being a superb wine stopper, cork is a unique and versatile material. Cork was used by ancient civilisations for millennia, and we are now rediscovering its incredible properties. It is light, impermeable, and used to produce everything from clothing to spacecrafts. Cork is har
From playlist Reel Ideas

🇬🇪 Georgia Road Trip Part 2- Rabati Castle in Akhaltsikhe (Ahıska)
After spending the night in Atskuri, we headed back to main town of Akhaltsikhe to explore and find something to eat. We directly went to the Rabati Castle before the tourist flocks flooded in. After the tour of the castle, we found a very small local bread makers selling lavash style of b
From playlist Travels around the World

Here is a model Stirling Engine made by my friend Izzet. It is a piece of art. I love to hear that engine sound. I hope you will like it too.
From playlist Izzet Özgöçmen

🇬🇪 Georgia Road Trip - Turkish Border to Akhaltsikhe via Akhalkalaki [Ahıska] [Part 1]
Right after passing the recently opened Turkish-Georgian border (so-called Aktaş Sınır Kapısı), we head towards Akhalkalaki. From there, we turned towards North to the curly canyon roads to reach Ahıska (Akhaltsikhe). Although the road is narrow and shared for both ways and sometimes with
From playlist Travels around the World

Abdurehim Heyit - Karşılaşınca (Anadolu Türkçesi ile altyazılı)
Abdurehim Heyit, büyük Uygur Türk şairi ve müzisyeni (Dikkat: Alt yazıları izlemek için "annotations" ayarı açık olmalıdır.) Türküde dile gelen genç kız, küskün bir vatanı temsil etmektedir. Abdurehim Heyit, Yunus Emre ve Aşık Veysel kadar büyük bir ozandır. Duruşu, samimiyeti ve sad
From playlist Instrumental Music

Mike Makes Moonshine Using Kudzu Vine & Cantaloupe! | Moonshiners
Mike makes a batch of moonshine using Kadzu, the infamous vine that ate the south! #discoveryplus #moonshiners Stream Full Episodes of Moonshiners https://www.discoveryplus.com/show/moonshiners About Moonshiners: Every spring, a fearless group of men and women venture deep into the woods
From playlist Recent Uploads

Classical and new plumbings bounding contractible manifolds and homology balls - Oğuz Şavk
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Topic: Classical and new plumbings bounding contractible manifolds and homology balls Speaker: Oğuz Şavk Affiliation: Boğaziçi University Date: May 28, 2021 A central problem in low-dimensional topology asks which homology
From playlist Mathematics

Around Hatay: Arsuz, Mediterranean, Ancient Titus Tunnels and Armenian Village #hatay #arsuz
To jump to drone footage: 29:10 Around Hatay: Arsuz, Mediterranean, Ancient Titus Tunnels and Armenian Village We continue our travel in Hatay and try to visit some of the tourist hot spots. Starting from our Iskenderun base, we drive to Hatay and visit the ancient Titus Tunnels and then
From playlist Turkey Travel 2022

7. Natural Honeycombs: Cork; Foams: Linear Elasticity
MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015 View the complete course: http://ocw.mit.edu/3-054S15 Instructor: Lorna Gibson This session begins with a look at cork as a natural honeycomb structure, and covers properties of foams and some modeling. Licens
From playlist MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015
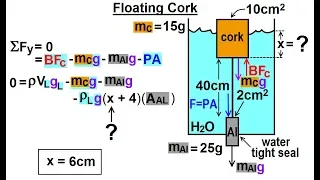
Physics - Ch 33A Test Your Knowledge: Fluid Statics (20 of 36) Floating Cork: VERY INTERESTING
Visit http://ilectureonline.com for more math and science lectures! In this video I will find the distance, x=?, from the water line to the bottom of the cork floating in jar of water with an aluminum water tight seal. To donate: http://www.ilectureonline.com/donate https://www.patreon.c
From playlist PHYSICS 33A TEST YOUR KNOWLEDGE: FLUID STATICS

CHW10.06 Cork Cube (Buoyant Force)
From playlist Problems | Fluid Mechanics

This week on Don't Be Dumb, Josh delivers you from committing a most embarrassing dining faux pas, by explaining the real purpose of restaurants offering you the cork from a freshly-opened bottle of wine. Tune in for new episodes of Don't Be Dumb every Thursday! Watch More Stuff You Shou
From playlist Stuff You Should Know

Particle Physics (14 of 41) Elementary Particles: What Is A Quark? (Part 2)
Visit http://ilectureonline.com for more math and science lectures! In this video I will describe the physical aspects of a quark. Next video in the Particle Physics series can be seen at: https://youtu.be/Tokfrq-aJVk
From playlist PHYSICS 65 PARTICLE PHYSICS

What is It? MYSTERY TOOL #39b answer tubalcain
Watch my many other shop videos. Also, see the playlist for the WHAT IS IT? series.
From playlist WHAT IS IT? MYSTERY TOOL

There's A Lot Of Science In That Wine Cork! See How They're Made!
#HowItsMade These high-tech stoppers are specially crafted to prevent musty odors. Full Episodes Streaming FREE: http://www.sciencechannel.com/tv-shows/how-its-made/ Subscribe to Science Channel: http://bit.ly/SubscribeScience Join Us on Facebook: https://www.facebook.com/ScienceChannel
From playlist How It's Made

Physics - Ch 33A Test Your Knowledge: Fluid Statics (37 of 42) Capillary Action: Measuring
Visit http://ilectureonline.com for more math and science lectures! What radius should the ring have for the surface tension of the water to keep the ring below the surface? (Neglect the weight of the wire.) To donate: http://www.ilectureonline.com/donate https://www.patreon.com/user?u=3
From playlist PHYSICS 33A TEST YOUR KNOWLEDGE: FLUID STATICS

SUPPORT CR on PATREON: http://bit.ly/2qBHcvf Chances are you've used a glass bottle just today – you could even be sipping out of one right now. While the modern glass bottle may seem boring and rather simple, they actually represent centuries of innovation in manufacturing and production
From playlist Concerning Engineering
