
How to Construct a Dodecahedron
How the greeks constructed the Dodecahedron. Euclids Elements Book 13, Proposition 17. In geometry, a dodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. A regular dode
From playlist Platonic Solids

Geometry: Ch 4 - Geometric Figures (16 of 18) The Right Circular Cone Truncated
Visit http://ilectureonline.com for more math and science lectures! In this video I will define the right circular truncated cone, and explain the equations of its surface area and volume. Next video in this series can be seen at: https://youtu.be/zNxXORWmA2E
From playlist GEOMETRY 4 - GEOMETRIC FIGURES

How to construct a Tetrahedron
How the greeks constructed the first platonic solid: the regular tetrahedron. Source: Euclids Elements Book 13, Proposition 13. In geometry, a tetrahedron also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. Th
From playlist Platonic Solids

This shows a 3d print of a mathematical sculpture I produced using shapeways.com. This model is available at http://shpws.me/q0PF.
From playlist 3D printing

These sculptures are joint work with Roice Nelson. They are available from shapeways.com at http://shpws.me/oNgi, http://shpws.me/oqOx and http://shpws.me/orB8.
From playlist 3D printing
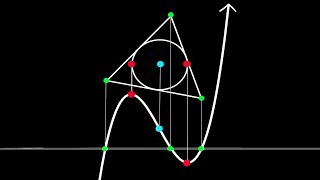
Solving a Cubic Equation Using a Triangle
There is this surprising fact about cubic equations with 3 real solutions where an equilateral triangle centered on the inflection point can always be scaled/rotated by some amount such that its vertices will line up with the roots of the equation. But is there any way that this can be us
From playlist Summer of Math Exposition Youtube Videos

An Introduction to Tensor Renormalization Group by Daisuke Kadoh
PROGRAM NONPERTURBATIVE AND NUMERICAL APPROACHES TO QUANTUM GRAVITY, STRING THEORY AND HOLOGRAPHY (HYBRID) ORGANIZERS: David Berenstein (University of California, Santa Barbara, USA), Simon Catterall (Syracuse University, USA), Masanori Hanada (University of Surrey, UK), Anosh Joseph (II
From playlist NUMSTRING 2022

Unified Theory of the Spiral Spin-liquids on Layered Honeycomb, Diamond... by Karlo Penc
PROGRAM FRUSTRATED METALS AND INSULATORS (HYBRID) ORGANIZERS Federico Becca (University of Trieste, Italy), Subhro Bhattacharjee (ICTS-TIFR, India), Yasir Iqbal (IIT Madras, India), Bella Lake (Helmholtz-Zentrum Berlin für Materialien und Energie, Germany), Yogesh Singh (IISER Mohali, In
From playlist FRUSTRATED METALS AND INSULATORS (HYBRID, 2022)

The Honeycombs of 4-Dimensional Bees ft. Joe Hanson | Infinite Series
Viewers like you help make PBS (Thank you 😃) . Support your local PBS Member Station here: https://to.pbs.org/donateinfi Be sure to check out It's OK to be Smart's video on nature's love of hexagons https://youtu.be/Pypd_yKGYpA And try CuriosityStream today: http://curiositystream.com/inf
From playlist Higher Dimensions

The Mysterious Architecture of the Universe - with J Richard Gott
J Richard Gott leads a journey through the history of our understanding of the Universe’s structure, and explains the ‘cosmic web’: the idea that our Universe is like a sponge made up of clusters of galaxies intricately connected by filaments of galaxies. Watch the Q&A here: https://youtu
From playlist Ri Talks
What are Cubic Graphs? | Graph Theory
What are cubic graphs? We go over this bit of graph theory in today's math lesson! Recall that a regular graph is a graph in which all vertices have the same degree. The degree of a vertex v is the number of edges incident to v, or equivalently the number of vertices adjacent to v. If ever
From playlist Graph Theory

Michael Weinstein - Discrete honeycombs, rational edges and edge states - IPAM at UCLA
Recorded 30 March 2022. Michael Weinstein of Columbia University, Applied Physics and Applied Mathematics, presents "Discrete honeycombs, rational edges and edge states" at IPAM's Multiscale Approaches in Quantum Mechanics Workshop. Abstract: We first discuss the derivation of tight bindin
From playlist 2022 Multiscale Approaches in Quantum Mechanics Workshop

7. Natural Honeycombs: Cork; Foams: Linear Elasticity
MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015 View the complete course: http://ocw.mit.edu/3-054S15 Instructor: Lorna Gibson This session begins with a look at cork as a natural honeycomb structure, and covers properties of foams and some modeling. Licens
From playlist MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015

Seminar In the Analysis and Methods of PDE (SIAM PDE): Michael Weinstein
Title: Effective Gaps for Time-Periodic Hamiltonians Modeling Floquet Materials Date: Thursday, February 2, 2023, 11:30 am EDT Speaker: Michael Weinstein, Columbia University Abstract: Floquet media are a type of material, in which time-periodic forcing is applied to alter the material’
From playlist Seminar In the Analysis and Methods of PDE (SIAM PDE)

Why do Bees build Hexagons? Honeycomb Conjecture explained by Thomas Hales
Mathematician Thomas Hales explains the Honeycomb Conjecture in the context of bees. Hales proved that the hexagon tiling (hexagonal honeycomb) is the most efficient way to maximise area whilst minimising perimeter. Interview with Oxford Mathematician Dr Tom Crawford. Produced by Tom Roc
From playlist Mathstars

Emergent Gauge Fields and Quantum Matter by G Baskaran
DISCUSSION MEETING : GEOMETRIC PHASES IN OPTICS AND TOPOLOGICAL MATTER ORGANIZERS : Subhro Bhattacharjee, Joseph Samuel and Supurna Sinha DATE : 21 January 2020 to 24 January 2020 VENUE : Madhava Lecture Hall, ICTS, Bangalore This is a joint ICTS-RRI Discussion Meeting on the geometric
From playlist Geometric Phases in Optics and Topological Matter 2020

MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015 View the complete course: http://ocw.mit.edu/3-054S15 Instructor: Lorna Gibson This session covers wood structure, micro-structure, stress-strain, honeycomb models, and bending. License: Creative Commons BY-NC
From playlist MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015

Cubic and Reciprocal Graphs: Find Cubic Equation From Sketch (2 Solutions) (Grade 9) - Maths
Topic: Cubic and Reciprocal Graphs: Find Cubic Equation From Sketch (2 Solutions) Do this paper online for free: https://www.onmaths.com/cubic-and-reciprocal-graphs/ Grade: 9 This question appears on calculator and non-calculator higher GCSE papers. Practise and revise with OnMaths. Go to
From playlist Cubic and Reciprocal Graphs

Dynamic Mass Generation in d=2 Dirac Fermions by Ribhu Kaul
DISCUSSION MEETING TOPOLOGICAL ASPECTS OF STRONG CORRELATIONS AND GAUGE THEORIES (ONLINE) ORGANIZERS: Rob Pisarski (Brookhaven National Laboratory, USA), Sumathi Rao (HRI, India), Soeren Schlichting (Bielefeld University, Germany) and Sayantan Sharma (IMSc, India) DATE: 06 September 202
From playlist Topological aspects of strong correlations and gauge theories (ONLINE)