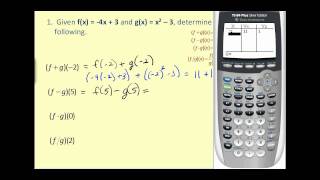
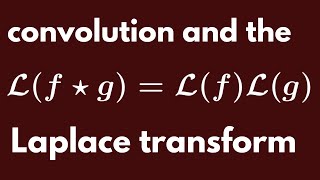Combinatorics | Theorems in discrete mathematics | Factorial and binomial topics
Star of David theorem
The Star of David theorem is a mathematical result on arithmetic properties of binomial coefficients. It was discovered by Henry W. Gould in 1972. (Wikipedia).