
Field Theory - Splitting Fields in CC - Lecture 11
In this video we compute some examples of splitting fields over CC. These include a Kummer field, a cyclotomic field, a quadratic field, and some real cubic field.
From playlist Field Theory
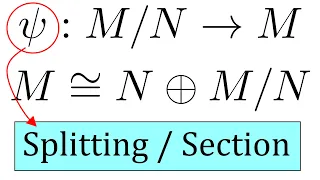
Splitting Homomorphism of R-Modules
A splitting, or section, is a homomorphism from the quotient module to the original module that gives a representative for each coset. If we have a splitting, we can prove that the module is isomorphic to a direct sum! This video is an explanation of how the splitting leads to an isomorphi
From playlist Ring & Module Theory

Dividing two exponents with rational powers to simplify the expression
👉 Learn how to divide with rational powers. To divide with numbers/expressions with rational exponents, we apply the basic rules of exponents. If the two numbers/expressions are the same, we simply take one of the number and raise it to the power of the difference between the exponents of
From playlist Divide Rational Exponents
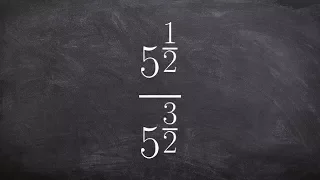
Dividing two exponents with fractional powers
👉 Learn how to divide with rational powers. To divide with numbers/expressions with rational exponents, we apply the basic rules of exponents. If the two numbers/expressions are the same, we simply take one of the number and raise it to the power of the difference between the exponents of
From playlist Divide Rational Exponents

👉 Learn how to simplify expressions by dividing its terms. Remember that dividing a fraction is the same as multiplying by the reciprocal. When multiplying expressions, each individual term of the expression is multiplied to its like term and the exponents is evaluated using the product ru
From playlist Simplify Using the Rules of Exponents | Divide Rational Expressions

👉 Learn how to simplify expressions by dividing its terms. Remember that dividing a fraction is the same as multiplying by the reciprocal. When multiplying expressions, each individual term of the expression is multiplied to its like term and the exponents is evaluated using the product ru
From playlist Simplify Using the Rules of Exponents | Divide Rational Expressions
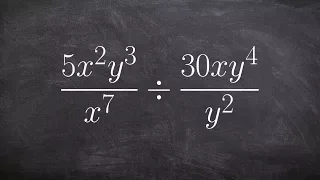
👉 Learn how to simplify expressions by dividing its terms. Remember that dividing a fraction is the same as multiplying by the reciprocal. When multiplying expressions, each individual term of the expression is multiplied to its like term and the exponents is evaluated using the product ru
From playlist Simplify Using the Rules of Exponents | Divide Rational Expressions

👉 Learn how to simplify expressions by dividing its terms. Remember that dividing a fraction is the same as multiplying by the reciprocal. When multiplying expressions, each individual term of the expression is multiplied to its like term and the exponents is evaluated using the product ru
From playlist Simplify Using the Rules of Exponents | Divide Rational Expressions

Dividing one rational monomial by another monomial and simplify
👉 Learn how to simplify expressions by dividing its terms. Remember that dividing a fraction is the same as multiplying by the reciprocal. When multiplying expressions, each individual term of the expression is multiplied to its like term and the exponents is evaluated using the product ru
From playlist Simplify Using the Rules of Exponents | Divide Rational Expressions

A non-linear spinor theory of elementary particles
This presentation is about a non-linear spinor theory of elementary particles developed by Norbert Winter, an elementary particle physicist and former employee of the Max-Planck Institute for Physics in Munich, Germany. The idea of a non-linear theory of elementary particles dates back to
From playlist Summer of Math Exposition Youtube Videos

Marc Levine: Refined enumerative geometry (Lecture 4)
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Lecture 4: Characteristic classes in Witt-cohomology Classical enumerative geometry relies heavily on the theory of Chern classes of vector bundles and the splitting principle, which
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Brain Teasers: 3. Pigeons, ants and occupancy
In this video we see an application of the (generalised) pigeonhole principle (https://en.wikipedia.org/wiki/Pigeonhole_principle).
From playlist Brain Teasers and Quant Interviews

Rico Zenklusen: Approximation algorithms for hard augmentation problems, lecture II
Augmentation Problems are a fundamental class of Network Design Problems. In short, the goal is to find a cheapest way to increase the (edge-)connectivity of a graph by adding edges from a given set of options. The Minimum Spanning Tree Problem is one of its most elementary examples, which
From playlist Summer School on modern directions in discrete optimization
H. Guenancia - A decomposition theorem for singular spaces with trivial canonical class (Part 2)
The Beauville-Bogomolov decomposition theorem asserts that any compact Kähler manifold with numerically trivial canonical bundle admits an étale cover that decomposes into a product of a torus, an irreducible, simply-connected Calabi-Yau, and holomorphic symplectic manifolds. With the deve
From playlist Ecole d'été 2019 - Foliations and algebraic geometry

The vacuum-gap transmon qubit: ultra-strong light (...)- G. Steele - PRACQSYS 2018 - CEB T2 2018
Gary Steele (Kavli Institute of Nanoscience, Delft University of Technology, Delft, The Netherlands) / 02.07.2018 The vacuum-gap transmon qubit: ultra-strong light matter coupling and insights into the physics of the Lamb shift In this talk, I will present our implementation of ultra-st
From playlist 2018 - T2 - Measurement and Control of Quantum Systems: Theory and Experiments

Where Are The Worlds In Many Worlds?
Sign Up on Patreon to get access to the Space Time Discord! https://www.patreon.com/pbsspacetime Many Worlds interpretation of quantum mechanics proposes that every time a quantum event gets decided, the universe splits so that every possible outcome really does occur. But where exactly a
From playlist Many Worlds and the Multiverse Explained!

Christophe Breuil - Espace de Drinfeld, complexe de de Rham...
Espace de Drinfeld, complexe de de Rham et représentations localement analytiques de GL3(Qp) Par un résultat de Dat, le complexe de de Rham de l'espace de Drinfeld (plus exactement ses sections globales) se scinde dans une catégorie dérivée convenable (i. e. est isomorphe à sa cohomologie
From playlist The Paris-London Number Theory Seminar, Oct. 2019

Chem 131A. Lec 16. Quantum Principles: Energy Level Diagrams, Spin-Orbit Coupling, Pauli Principle
UCI Chem 131A Quantum Principles (Winter 2014) Lec 16. Quantum Principles -- Energy Level Diagrams, Spin-Orbit Coupling, Pauli Principle -- View the complete course: http://ocw.uci.edu/courses/chem_131a_quantum_principles.html Instructor: A.J. Shaka, Ph.D License: Creative Commons BY-NC-
From playlist Chem 131A: Week 6

Representations of finite groups of Lie type (Lecture 2) by Dipendra Prasad
PROGRAM : GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fun
From playlist Group Algebras, Representations And Computation

Divide using synthetic division and check with remainder theorem
👉 Learn about dividing by synthetic division when there is a missing power. Synthetic division is a method of dividing polynomials by linear expressions. To divide using synthetic division, we equate the divisor to 0 and then solve for the variable, the solution for the variable will be th
From playlist Divide Polynomials using Synthetic Division