
From playlist Courses and Series

The Nature of Causation: The Counterfactual Theory of Causation
In this second lecture in this series on the nature of causation, Marianne Talbot discusses the counterfactual theory of causation. We have causal theories of reference, perception, knowledge, content and numerous other things. If it were to turn out that causation doesn’t exist, we would
From playlist The Nature of Causation

The idea of ‘atonement’ sounds very old-fashioned and is deeply rooted in religious tradition. To atone means, in essence, to acknowledge one’s capacity for wrongness and one’s readiness for apology and desire for change. It’s a concept that every society needs at its center. For gifts and
From playlist RELATIONSHIPS

How an Equilibrium Constant varies with Temperature - Thermodynamics - Physical Chemistry
Deriving a quantitative relationship to show how an equilibrium constant varies with temperature and so showing were Le Chatelier's Principle comes from in this context. Along the way, the Gibbs-Helmholtz van't Hoff equations are derived and used. My video for deriving the thermodynamics
From playlist Introductory Thermodynamics

The Nature of Causation: The Necessary Connection Analysis
In this third lecture in this series on the nature of causation, Marianne Talbot discusses the necessary connection analysis of causation. We have causal theories of reference, perception, knowledge, content and numerous other things. If it were to turn out that causation doesn’t exist, w
From playlist The Nature of Causation

From playlist Level 2 NCEA Physics

Math 131 Fall 2018 100818 Limits and Continuity in Metric Spaces
Limits of functions (in the setting of metric spaces). Definition. Rephrasal of definition. Uniqueness of limit. Definition of continuity at a point. Remark on continuity at an isolated point. Relation with limits. Composition of continuous functions is continuous. Alternate (topol
From playlist Course 7: (Rudin's) Principles of Mathematical Analysis (Fall 2018)

CTNT 2020 - Elliptic curves and the local-global principle for quadratic forms - Asher Auel
The Connecticut Summer School in Number Theory (CTNT) is a summer school in number theory for advanced undergraduate and beginning graduate students, to be followed by a research conference. For more information and resources please visit: https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2020 - Conference Videos

A positive proportion of plane cubics fail the Hasse principle - Manjul Bhargava [2011]
Arithmetic Statistics April 11, 2011 - April 15, 2011 April 11, 2011 (02:10 PM PDT - 03:00 PM PDT) Speaker(s): Manjul Bhargava (Princeton University) Location: MSRI: Simons Auditorium http://www.msri.org/workshops/567/schedules/12761
From playlist Number Theory

Haowen Zhang - Brauer-Manin and cohomological obstructions to rational points
In the problem of deciding integer or rational solutions of polynomial equations (i.e. finding integer/rational points of a variety), we often first look at the “local” solutions over all the Q_p. When does a collection of local solutions give rise to an honest global solution over Q? Ther
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Minhyong Kim: Recent progress on the effective Mordell problem
SMRI Algebra and Geometry Online: Minhyong Kim (University of Warwick) Abstract: In 1983, Gerd Faltings proved the Mordell conjecture stating that curves of genus at least two have only finitely many rational points. This can be understood as the statement that most polynomial equations
From playlist SMRI Algebra and Geometry Online

The Problem With Perfectionism
We aim for perfection without a correct idea of what perfection might demand from us. To strengthen our resolve, we need to improve our picture of what sacrifices any achievement will demand. If you like our films, take a look at our shop (we ship worldwide): https://goo.gl/p8kdj3 Join ou
From playlist SELF

Introduction to h-principle by Mahuya Datta
DATE & TIME: 25 December 2017 to 04 January 2018 VENUE: Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex structure. The moduli space of these curves (
From playlist J-Holomorphic Curves and Gromov-Witten Invariants

Flexibilization as localization - Oleg Lazarev
Workshop on the h-principle and beyond Topic: Flexibilization as localization Speaker: Oleg Lazarev Affiliation: University of Massachusetts, Boston Date: November 5, 2021 Abstract: Cieliebak and Eliashberg showed that there is a special class of flexible symplectic structures that sati
From playlist Mathematics

Christopher Frei: Constructing abelian extensions with prescribed norms
CIRM VIRTUAL CONFERENCE Recorded during the meeting " Diophantine Problems, Determinism and Randomness" the November 24, 2020 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide
From playlist Virtual Conference
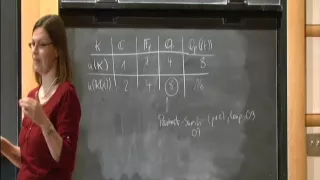
Patching and Local-Global Principles - Julia Hartmann
Julia Hartmann RWTH Aachen University; Member, School of Mathematics November 5, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

Local-Global principles for tori over arithmetic surfaces - Hartmann - Workshop 1 - CEB T2 2019
Julia Hartmann (University of Pennsylvania) / 22.05.2019 Local-Global principles for tori over arithmetic surfaces Given a field F and a collection of overfields Fi (i ∈ I), we say that the local global principle holds for an F-variety Z if the existence of a rational point over each Fi
From playlist 2019 - T2 - Reinventing rational points

Teach Astronomy - Observing the Universe
http://www.teachastronomy.com/ The strong version of the anthropic principle in essence states that the observed values of physical and cosmological quantities are not accidents but are connected somehow with our existence as observers of the universe. The universe was built for us. This
From playlist 29. Prospects of Nonhuman Intelligences

