Powered by https://www.numerise.com/ Gradient of a line segment 1
From playlist Linear sequences & straight lines

How explained Slinky down stairs!!!
In this video i show and explained slinky move down stairs!
From playlist MECHANICS

going over and over and over the gradient and y intercept idea
From playlist 2014 9mat

Beginner Yoga Tutorial 4 - Warrior Two, Plank, Downward Dog
In this 4th yoga tutorial, we show you how to get to warrior two from Downward dog. The whole sequence is: Table top - Plank - Downward dog - Single legged downward dog - Lung forward - Warrior two. And then we show you how to get back to the original position and then repeat with the othe
From playlist Yoga

Arithmetic statistics and graded Lie algebras - Jef Laga
Joint IAS/Princeton University Number Theory Seminar Topic: Arithmetic statistics and graded Lie algebras Speaker: Jef Laga Affiliation: University of Cambridge Date: March 17, 2022 I will explain how various results in arithmetic statistics by Bhargava, Gross, Shankar and others on 2-Se
From playlist Mathematics

Introduction to Fiber Bundles Part 4: Torsor Interlude
Torsors and Principal Homogeneous Spaces. What is the difference?
From playlist Fiber bundles

THE FIGURE: Foreshortening and the figure (3 of 3)
Marc takes on a head forward figure in foreshortening.
From playlist THE FIGURE

Jean-Baptiste Teyssier: Skeletons and moduli of Stokes torsors
Abstract: In the local classification of differential equations of one complex variable, torsors under a certain sheaf of algebraic groups (the Stokes sheaf) play a central role. On the other hand, Deligne defined in positive characteristic a notion of skeletons for l-adic local systems on
From playlist Analysis and its Applications

Wei Ho: Explicit models of genus one curves and related problems
CIRM HYBRID EVENT We discuss various explicit models of genus one curves, some classical and some a little less so, with an eye towards applications in number theory and arithmetic geometry. In particular, we will talk about how understanding such models has shed light on many kinds of pro
From playlist Algebraic and Complex Geometry

Parahoric torsors, parabolic bundles and applications by Vikraman Balaji
DISCUSSION MEETING : MODULI OF BUNDLES AND RELATED STRUCTURES ORGANIZERS : Rukmini Dey and Pranav Pandit DATE : 10 February 2020 to 14 February 2020 VENUE : Ramanujan Lecture Hall, ICTS, Bangalore Background: At its core, much of mathematics is concerned with the problem of classif
From playlist Moduli Of Bundles And Related Structures 2020

Digression: The cotangent complex and obstruction theory
We study the cotangent complex more in depth and explain its relation to obstruction theory. As an example we construct the Witt vectors of a perfect ring. This video is a slight digression from the rest of the lecture course and could be skipped. Feel free to post comments and questions
From playlist Topological Cyclic Homology
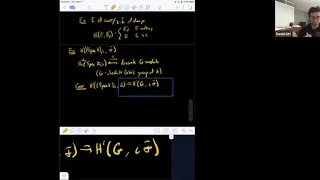
Étale Cohomology - September 17, 2020
Čech cohomology for fields, torsors and H^1, Hilbert's theorem 90
From playlist Étale cohomology and the Weil conjectures

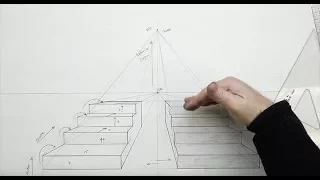
FORMAL LINEAR PERSPECTIVE: SECTION TWO-STAIRS: Ex.#20-23
More stairs. (one small editing glitch-you'll see, but otherwise solid video)
From playlist FORMAL LINEAR PERSPECTIVE

Charles Rezk - 4/4 Higher Topos Theory
Course at the school and conference “Toposes online” (24-30 June 2021): https://aroundtoposes.com/toposesonline/ Slides: https://aroundtoposes.com/wp-content/uploads/2021/07/RezkNotesToposesOnlinePart4.pdf In this series of lectures I will give an introduction to the concept of "infinity
From playlist Toposes online

Calculus 1 - Derivatives and Related Rates (14 of 24) Sliding Ladder: Example 2
Visit http://ilectureonline.com for more math and science lectures! I this video I will calculate the height of a ladder resting against a wall when the ladder is sliding down. Next video in this series can be seen at: https://youtu.be/aPKGndMLJ2g
From playlist CALCULUS 1 CH 6.5 RELATED RATES

Yuri Tschinkel, Height zeta functions
VaNTAGe seminar May 11, 2021 License: CC-BY-NC-SA
From playlist Manin conjectures and rational points

Beginner Yoga Tutorial 3 - Cobra to Plank to Downward Dog
So in this tutorial we work on how to transition from Cobra to plank to downward dog and vice versa. This is a good move that stretches your lower back. Try it!
From playlist Yoga

Brauer groups, Severi-Brauer schemes, Azumaya algebras, twisted sheaves
From playlist Étale cohomology and the Weil conjectures
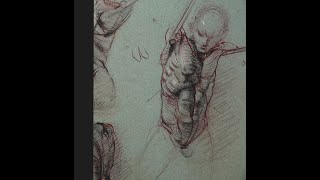
ANATOMY FOR ARTISTS: The Torso anatomy demonstrations Part 2
More torso demonstrations with figure models redacted.
From playlist ANATOMY FOR ARTISTS