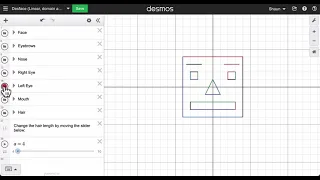
Here we show a quick way to set up a face in desmos using domain and range restrictions along with sliders. @shaunteaches
From playlist desmos

MATH331: Riemann Surfaces - part 1
We define what a Riemann Surface is. We show that PP^1 is a Riemann surface an then interpret our crazy looking conditions from a previous video about "holomorphicity at infinity" as coming from the definition of a Riemann Surface.
From playlist The Riemann Sphere

Quick tips for setting up a line in desmos from a point and slope
From playlist desmos

Sections of del Pezzo fibrations over P1 - Tanimoto - Workshop 1 - CEB T2 2019
Sho Tanimoto (Kumamoto University, Japan) / 20.05.2019 Sections of del Pezzo fibrations over P1 Mori’s Bend and Break shows that if we deform a rational curve while fixing two points, then it breaks into the union of rational curves. However, in general it is difficult to control the nu
From playlist 2019 - T2 - Reinventing rational points

ANATOMY FOR ARTISTS: The Pelvis-Constructions and general parts to know for drawing
Marc describes and draws the pelvis and looks at ways to draw the form by simplifying it into either a box or bowl form.
From playlist ANATOMY FOR ARTISTS

Complex surfaces 3: Rational surfaces
We give an informal survey of some complex rational surfaces. We first lift a few examples: hypersurfaces of degree at most 3, and the Hirzebruch surfaces which are P1 bundles over P1. Then we discuss the surfaces obtained by blowing up points in the plane in more detail. We sketch how to
From playlist Algebraic geometry: extra topics
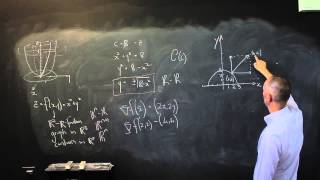
11_6_1 Contours and Tangents to Contours Part 1
A contour is simply the intersection of the curve of a function and a plane or hyperplane at a specific level. The gradient of the original function is a vector perpendicular to the tangent of the contour at a point on the contour.
From playlist Advanced Calculus / Multivariable Calculus

Marcello Bernardara: Semiorthogonal decompositions and birational geometry of geometrically rational
Abstract:This is a joint work in progress with A. Auel. Let S be a geometrically rational del Pezzo surface over a field k. In this talk, I will show how the k-rationality of S is equivalent to the existence of some semiorthogonal decompositions of its derived category. In particular, the
From playlist HIM Lectures: Junior Trimester Program "Algebraic Geometry"

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Persistence of the Brauer-Manin obstruction under field extension - Viray - Workshop 2 - CEB T2 2019
Bianca Viray (University of Washington) / 27.06.2019 Persistence of the Brauer-Manin obstruction under field extension. We consider the question of when an empty Brauer set over the ground field gives rise to an empty Brauer set over an extension. We first consider the case of quartic d
From playlist 2019 - T2 - Reinventing rational points

What is the difference between convex and concave
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Alessio Corti: Mirror symmetry for orbifold del Pezzo surfaces
I will state some interconnected conjectures on (a) the algebraic geometry and moduli spaces, and (b) mirror symmetry, for orbifolds del Pezzo surfaces. I will present some of the evidence. This is joint work in progress with many people and students of the PRAGMATIC school held last Summe
From playlist HIM Lectures: Junior Trimester Program "Algebraic Geometry"

Rational cuspidal curves on del-Pezzo surfaces by Ritwik Mukherjee
Higgs bundles URL: http://www.icts.res.in/program/hb2016 DATES: Monday 21 Mar, 2016 - Friday 01 Apr, 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore DESCRIPTION: Higgs bundles arise as solutions to noncompact analog of the Yang-Mills equation. Hitchin showed that irreducible solutio
From playlist Higgs Bundles

A birational model of the Cartwright-Steger surface - Igor Dolgachev
Igor Dolgachev University of Michigan January 21, 2015 A Cartwright-Steger surface is a complex ball quotient by a certain arithmetic cocompact group associated to the cyclotomic field Q(e2πi/12)Q(e2πi/12), its numerical invariants are with c21=3c2=9,pg=q=1c12=3c2=9,pg=q=1. It is a cyclic
From playlist Mathematics

What is the difference between convex and concave polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Fabrizio Catanese: New examples of rigid varieties and criteria for fibred surfaces [...]
Abstract: Given an algebraic variety defined by a set of equations, an upper bound for its dimension at one point is given by the dimension of the Zariski tangent space. The infinitesimal deformations of a variety X play a somehow similar role, they yield the Zariski tangent space at the
From playlist Algebraic and Complex Geometry

Isosceles Triangle Theorem: Dynanic Desmos Illustrator
Isosceles triangle theorem animation & explorer made in #Desmos. https://teacher.desmos.com/activitybuilder/custom/60742b18afd8ae0d274b6efb #MTBoS #ITeachMath #math
From playlist Desmos Activities, Illustrations, and How-To's

Positivity and algebraic integrability of holomorphic foliations – Carolina Araujo – ICM2018
Algebraic and Complex Geometry Invited Lecture 4.7 Positivity and algebraic integrability of holomorphic foliations Carolina Araujo Abstract: The theory of holomorphic foliations has its origins in the study of differential equations on the complex plane, and has turned into a powerful t
From playlist Algebraic & Complex Geometry

What is the difference between concave and convex polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons
