
What Are Allotropes of Metalloids and Metals | Properties of Matter | Chemistry | FuseSchool
What Are Allotropes of Metalloids and Metals Learn the basics about allotropes of metalloids and metals, as a part of the overall properties of matter topic. An allotrope is basically a different form of the same element, each with distinct physical and chemical properties. For example
From playlist CHEMISTRY

Chemistry - Liquids and Solids (44 of 59) Crystal Structure: Covalent: Metallic
Visit http://ilectureonline.com for more math and science lectures! In this video I explain the metallic crystal structure.
From playlist CHEMISTRY 16 LIQUIDS AND SOLIDS

Mod-01 Lec-8 Cohesion in Solids
Condensed Matter Physics by Prof. G. Rangarajan, Department of Physics, IIT Madras. For more details on NPTEL visit http://nptel.iitm.ac.in
From playlist NPTEL: Condensed Matter Physics - CosmoLearning.com Physics Course
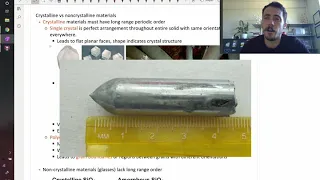
Crystalline vs Amorphous materials
Materials are either crystalline or amorphous. They contain long-range periodic order or they do not. This leads to very different properties! Crystalline materials can be either polycrystalline or single crystal in nature. we can see evidence of single crystals in faceting of crystal face
From playlist Materials Sciences 101 - Introduction to Materials Science & Engineering 2020

Chemistry - Liquids and Solids (45 of 59) Crystal Structure: Covalent: Glass
Visit http://ilectureonline.com for more math and science lectures! In this video I explain the glass crystal structure and amorphous solids.
From playlist CHEMISTRY 16 LIQUIDS AND SOLIDS

Ionic Solids, Molecular Solids, Metallic Solids, Network Covalent Solids, & Atomic Solids
This chemistry video tutorial provides a basic introduction into solids. It explains how to classify a solid as ionic solids, molecular solids or atomic solids. There are 3 different types of atomic solids that you need to be familiary with - metallic solids, Group 8A solids, and network
From playlist New AP & General Chemistry Video Playlist

Covalent Compounds: Writing Chemical Names and Formulas
How to write the chemical names and formulas for covalent compounds. You can see a listing of all my videos at my website, http://www.stepbystepscience.com
From playlist Chemical Equations; Ionic and Covalent Compounds
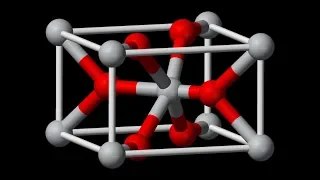
Lattice Structures in Ionic Solids
We've learned a lot about covalent compounds, but we haven't talked quite as much about ionic compounds in their solid state. These will adopt a highly ordered and repeating lattice structure, but the geometry of the lattice depends entirely on the types of ions and their ratio in the chem
From playlist General Chemistry

Courses on Khan Academy are always 100% free. Start practicing—and saving your progress—now: https://www.khanacademy.org/science/chemistry/chemical-bonds/x822131fc:bond-energy/v/ionic-bonds-and-coulombs-law Introduction to how the strength of ionic bonds is related to Coulomb's law. Exam
From playlist Chemistry

Christian Liedtke: Crystalline cohomology, period maps, and applications to K3 surfaces
Abstract: I will first introduce K3 surfaces and determine their algebraic deRham cohomology. Next, we will see that crystalline cohomology (no prior knowledge assumed) is the "right" replacement for singular cohomology in positive characteristic. Then, we will look at one particular class
From playlist Algebraic and Complex Geometry

B. Bhatt - Prisms and deformations of de Rham cohomology
Prisms are generalizations of perfectoid rings to a setting where "Frobenius need not be an isomorphism". I will explain the definition and use it to construct a prismatic site for any scheme. The resulting prismatic cohomology often gives a one-parameter deformation of de Rham cohomology.
From playlist Arithmetic and Algebraic Geometry: A conference in honor of Ofer Gabber on the occasion of his 60th birthday

Lance Gurney: The geometric approach to cohomology Part II
SMRI Seminar Course: 'The geometric approach to cohomology' Part II Lance Gurney (Australian National University) Abstract: The aim of these two talks is to give an overview of the geometric aka stacky approach to various cohomology theories for schemes: de Rham, Hodge, crystalline and p
From playlist SMRI Course: The geometric approach to cohomology

A Gentle Approach to Crystalline Cohomology - Jacob Lurie
Members’ Colloquium Topic: A Gentle Approach to Crystalline Cohomology Speaker: Jacob Lurie Affiliation: Professor, School of Mathematics Date: February 28, 2022 Let X be a smooth affine algebraic variety over the field C of complex numbers (that is, a smooth submanifold of C^n which can
From playlist Mathematics

James Borger: The geometric approach to cohomology Part I
SMRI Seminar Course: 'The geometric approach to cohomology' Part I James Borger (Australian National University) Abstract: The aim of these two talks is to give an overview of the geometric aka stacky approach to various cohomology theories for schemes: de Rham, Hodge, crystalline and pr
From playlist SMRI Course: The geometric approach to cohomology

Derived de Rham Cohomology - Bhargav Bhatt
Bhargav Bhatt University of Michigan; Member, School of Mathematics September 25, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

Takeshi Tsuji: On p-adic étale cohomology of perverse sheaves
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

Pierre Berthelot - Non characteristic finiteness theorems in crystalline cohomology
On the crystalline site relative to Z/p^n, I will explain the construction of two triangulated subcategories of the derived category of complexes of filtered modules on the structural sheaf, linked by a local biduality theorem. For these complexes, one can prove finiteness theorems for inv
From playlist A conference in honor of Arthur Ogus on the occasion of his 70th birthday
p-adic approaches to rational points on curves - Poonen - Lecture 3/4 - CEB T2 2019
Bjorn Poonen (Massachusetts Institute of Technology) / 08.07.2019 p-adic approaches to rational points on curves - Lecture 3/4 In these four lectures, I will describe Chabauty's p-adic method for determining the rational points on a curve whose Jacobian has rank less than the genus, hint
From playlist 2019 - T2 - Reinventing rational points

Ionic and Covalent Compounds: Writing Names and Formulas
Describes how to write names and formulas for ionic compounds and covalent compounds. You can see a listing of all my videos at my website, http://www.stepbystepscience.com
From playlist Chemical Equations; Ionic and Covalent Compounds

Introduction to p-adic Hodge theory (Lecture 4) by Denis Benois
PROGRAM PERFECTOID SPACES ORGANIZERS: Debargha Banerjee, Denis Benois, Chitrabhanu Chaudhuri, and Narasimha Kumar Cheraku DATE & TIME: 09 September 2019 to 20 September 2019 VENUE: Madhava Lecture Hall, ICTS, Bangalore Scientific committee: Jacques Tilouine (University of Paris, France
From playlist Perfectoid Spaces 2019