How to Prove a Function is Not an Open Function
How to Prove a Function is Not an Open Function If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Thank you:)
From playlist Topology
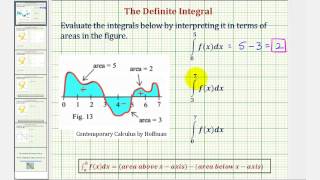
Ex: Definite Integrals as Area Given a Graph (Function)
This video explains how to evaluate a definite integral given the graph of a function and the area bounded by the function and the x-axis. The function is above and below the x-axis. Site: http://mathispower4u
From playlist Definite Integrals and The Fundamental Theorem of Calculus

Calculus - The Fundamental Theorem, Part 5
The Fundamental Theorem of Calculus. How an understanding of an incremental change in area helps lead to the fundamental theorem
From playlist Calculus - The Fundamental Theorem of Calculus

My notes are available at http://asherbroberts.com/ (so you can write along with me). Calculus: Early Transcendentals 8th Edition by James Stewart
From playlist Calculus

Workshop 1 "Operator Algebras and Quantum Information Theory" - CEB T3 2017 - M.Brannan
Michael Brannan (College station) / 12.09.17 Title: Entangled subspaces from quantum groups and their associated quantum channels. Abstract:I will describe a class of highly entangled subspaces of bipartite quantum systems arising from the representation theory of a class of compact quan
From playlist 2017 - T3 - Analysis in Quantum Information Theory - CEB Trimester

Workshop 1 "Operator Algebras and Quantum Information Theory" - CEB T3 2017 - M.Musat
Magdalena Musat (University of Copenhagen) / 14.09.17 Title: Quantum correlations, tensor norms, and factorizable quantum channels Abstract: In joint work with Haagerup, we established in 2015 a reformulation of the Connes embedding problem in terms of an asymptotic property of quantum c
From playlist 2017 - T3 - Analysis in Quantum Information Theory - CEB Trimester
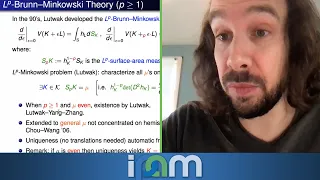
Emanuel Milman - The log-Minkowski Problem - IPAM at UCLA
Recorded 09 February 2022. Emanuel Milman of Technion - Israel Institute of Technology presents "The log-Minkowski Problem" at IPAM's Calculus of Variations in Probability and Geometry Workshop. Abstract: The classical Minkowski problem asks to find a convex body K in Rn having a prescrib
From playlist Workshop: Calculus of Variations in Probability and Geometry

Workshop 1 "Operator Algebras and Quantum Information Theory" - CEB T3 2017 - A.Gheondea
Aurelian Gheondea (Bilkent University, Ankara) / 11.09.17 Title: Symmetry versus Conservation Laws in Dynamical Quantum Systems: A Unifying Approach through Propagation of Fixed Points Abstract: We unify recent Noether type theorems on the equivalence of symmetries with conservation laws
From playlist 2017 - T3 - Analysis in Quantum Information Theory - CEB Trimester
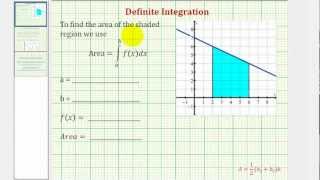
Ex: Setting Up a Definite Integral To Determine Area Under a Function
This video provides an example of how to set up a definite integral to determine the area under a function. The area is found using a geometric formula. http://mathispower4u.com
From playlist Definite Integrals and The Fundamental Theorem of Calculus

algebraic geometry 30 The Ax Grothendieck theorem
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It covers the Ax-Grothendieck theorem, which states that an injective regular map between varieties is surjective. The proof uses a strange technique: first prove the resu
From playlist Algebraic geometry I: Varieties
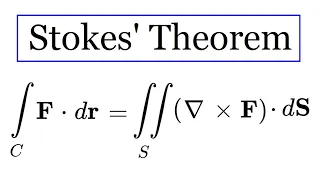
In this video, I present another example of Stokes theorem, this time using it to calculate the line integral of a vector field. It is a very useful theorem that arises a lot in physics, for example in Maxwell's equations. Other Stokes Example: https://youtu.be/-fYbBSiqvUw Yet another Sto
From playlist Vector Calculus

A quantitative inverse theorem for the U⁴ norm (...) - T. Gowers - Workshop 1 - CEB T1 2018
Timothy Gowers (Cambridge) / 02.02.2018 A quantitative inverse theorem for the U⁴ norm over finite fields The U⁴ norm is one of a sequence of norms that measure ever stronger forms of quasirandomness. The structure of bounded functions whose Uᵏ norms are within a constant of being as lar
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

F. Schulze - An introduction to weak mean curvature flow 4
It has become clear in recent years that to understand mean curvature flow through singularities it is essential to work with weak solutions to mean curvature flow. We will give a brief introduction to smooth mean curvature flow and then discuss Brakke flows, their basic properties and how
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics
Kristin Courtney: C*-structure on images of completely positive order zero maps
Talk by Kristin Courtney in Global Noncommutative Geometry Seminar (Americas) http://www.math.wustl.edu/~xtang/NCG-Seminar.html on September 16, 2020.
From playlist Global Noncommutative Geometry Seminar (Americas)

F. Schulze - An introduction to weak mean curvature flow 2 (version temporaire)
It has become clear in recent years that to understand mean curvature flow through singularities it is essential to work with weak solutions to mean curvature flow. We will give a brief introduction to smooth mean curvature flow and then discuss Brakke flows, their basic properties and how
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

F. Schulze - An introduction to weak mean curvature flow 2
It has become clear in recent years that to understand mean curvature flow through singularities it is essential to work with weak solutions to mean curvature flow. We will give a brief introduction to smooth mean curvature flow and then discuss Brakke flows, their basic properties and how
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Princeton/IAS Symplectic Geometry Seminar - Keon Choi
Keon Choi University of California, Berkeley March 7, 2014 Embedded contact homology is an invariant of a contact three-manifold, which is recently shown to be isomorphic to Heegaard Floer homology and Seiberg-Witten Floer homology. However, ECH chain complex depends on the contact form on
From playlist Mathematics

Ex: Definite Integrals as Area Given a Graph (Function + Constant)
This video explains how to evaluate a definite integral given the graph of a function and the area bounded by the function and the x-axis. The function is above and below the x-axis. Site: http://mathispower4u
From playlist Definite Integrals and The Fundamental Theorem of Calculus

F. Schulze - An introduction to weak mean curvature flow 3 (version temporaire)
It has become clear in recent years that to understand mean curvature flow through singularities it is essential to work with weak solutions to mean curvature flow. We will give a brief introduction to smooth mean curvature flow and then discuss Brakke flows, their basic properties and how
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics