
Find the value of the trigonometric expression using inverse
👉 Learn how to evaluate an expression with the composition of a function and a function inverse. Just like every other mathematical operation, when given a composition of a trigonometric function and an inverse trigonometric function, you first evaluate the one inside the parenthesis. We
From playlist Evaluate a Composition of Inverse Trigonometric Functions

Evaluate the composition of sine and sine inverse
👉 Learn how to evaluate an expression with the composition of a function and a function inverse. Just like every other mathematical operation, when given a composition of a trigonometric function and an inverse trigonometric function, you first evaluate the one inside the parenthesis. We
From playlist Evaluate a Composition of Inverse Trigonometric Functions

Illustrates the solution of a Bernoulli first-order differential equation. Free books: http://bookboon.com/en/differential-equations-with-youtube-examples-ebook http://www.math.ust.hk/~machas/differential-equations.pdf
From playlist Differential Equations with YouTube Examples

Differential Isomorphism and Equivalence of Algebraic Varieties Board at 49:35 Sum_i=1^N 2/(x-phi_i(y,t))^2
From playlist Fall 2017
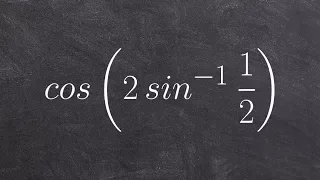
Evaluating the composition of cosine and sine inverse
👉 Learn how to evaluate an expression with the composition of a function and a function inverse. Just like every other mathematical operation, when given a composition of a trigonometric function and an inverse trigonometric function, you first evaluate the one inside the parenthesis. We
From playlist Evaluate a Composition of Inverse Trigonometric Functions

Gianluca Paolini: Torsion-free Abelian groups are Borel complete
HYBRID EVENT Recorded during the meeting "XVI International Luminy Workshop in Set Theory" the September 14, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicia
From playlist Logic and Foundations

Natasha Dobrinen: Borel sets of Rado graphs are Ramsey
The Galvin-Prikry theorem states that Borel partitions of the Baire space are Ramsey. Thus, given any Borel subset $\chi$ of the Baire space and an infinite set $N$, there is an infinite subset $M$ of $N$ such that $\left [M \right ]^{\omega }$ is either contained in $\chi$ or disjoint fr
From playlist Combinatorics
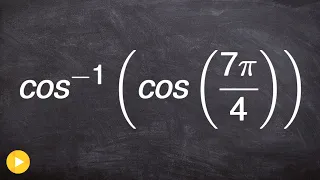
How to evaluate for the composition of two trigonometric functions
👉 Learn how to evaluate an expression with the composition of a function and a function inverse. Just like every other mathematical operation, when given a composition of a trigonometric function and an inverse trigonometric function, you first evaluate the one inside the parenthesis. We
From playlist Evaluate a Composition of Inverse Trigonometric Functions

Uri Bader - 1/4 Algebraic Representations of Ergodic Actions
Ergodic Theory is a powerful tool in the study of linear groups. When trying to crystallize its role, emerges the theory of AREAs, that is Algebraic Representations of Ergodic Actions, which provides a categorical framework for various previously studied concepts and methods. Roughly, this
From playlist Uri Bader - Algebraic Representations of Ergodic Actions

Finding the bearing of a plane using trigonometry
👉 Learn how to solve the word problems with trigonometry. Word problems involving angles, including but not limited to: bearings, angle of elevations and depressions, triangles problems etc are solved using trigonometry. To be able to solve these problems it is important that you have a gr
From playlist Evaluate Inverse Trigonometric Functions
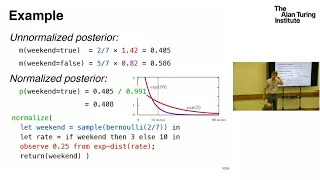
Semantic models for higher-order Bayesian inference - Sam Staton, University of Oxford
In this talk I will discuss probabilistic programming as a method of Bayesian modelling and inference, with a focus on fully featured probabilistic programming languages with higher order functions, soft constraints, and continuous distributions. These languages are pushing the limits of e
From playlist Logic and learning workshop

Introduction to Inverse Trigonometric Functions (Precalculus - Trigonometry 17)
What Inverse Trigonometric Functions are, where they come from, and why we need to restrict domain to be able to use them. Special focus will be on the nature of one-to-one functions and how they relate to the common trigonometric functions. Support: https://www.patreon.com/ProfessorLeona
From playlist Precalculus - College Algebra/Trigonometry

Kęstutis Česnavičius - Grothendieck–Serre in the quasi-split unramified case
Correction: The affiliation of Lei Fu is Tsinghua University. The Grothendieck–Serre conjecture predicts that every generically trivial torsor under a reductive group scheme G over a regular local ring R is trivial. We settle it in the case when G is quasi-split and R is unramified. To ov
From playlist Conférence « Géométrie arithmétique en l’honneur de Luc Illusie » - 5 mai 2021

What is the limit of a sequence of graphs?? | Benjamini-Schramm Convergence
This is an introduction to the mathematical concept of Benjamini-Schramm convergence, which is a type of graph limit theory which works well for sparse graphs. We hope that most of it is understandable by a wide audience with some mathematical background (including some prior exposure to g
From playlist Summer of Math Exposition Youtube Videos
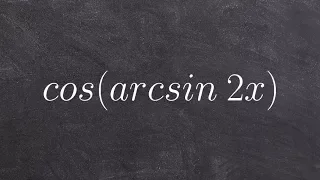
Evaluating the composition of inverse functions trigonometry
👉 Learn how to evaluate an expression with the composition of a function and a function inverse. Just like every other mathematical operation, when given a composition of a trigonometric function and an inverse trigonometric function, you first evaluate the one inside the parenthesis. We
From playlist Evaluate a Composition of Inverse Trigonometric Functions

Solve a Bernoulli Differential Equation (Part 2)
This video provides an example of how to solve an Bernoulli Differential Equation. The solution is verified graphically. Library: http://mathispower4u.com
From playlist Bernoulli Differential Equations

Leslie Saper : L2-cohomology and the theory of weights
Abstract : The intersection cohomology of a complex projective variety X agrees with the usual cohomology if X is smooth and satisfies Poincare duality even if X is singular. It has been proven in various contexts (and conjectured in more) that the intersection cohomology may be represente
From playlist Topology

Mazur's program B. - Zureick-Brown - Workshop 2 - CEB T2 2019
David Zureick-Brown (Emory University, Atlanta USA) / 25.06.2019 Mazur's program B. I’ll discuss recent progress on Mazur’s “Program B” – the problem of classifying all possibilities for the “image of Galois” for an elliptic curve over Q (equivalently, classification of all rational poi
From playlist 2019 - T2 - Reinventing rational points

An ergodic approach towards an equidistribution result of Ferrero–Washington by Bharathwaj Palvannan
PROGRAM ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (HYBRID) ORGANIZERS: Ashay Burungale (CalTech/UT Austin, USA), Haruzo Hida (UCLA), Somnath Jha (IIT Kanpur) and Ye Tian (MCM, CAS) DATE: 08 August 2022 to 19 August 2022 VENUE: Ramanujan Lecture Hall and online The program pla
From playlist ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (2022)

Evaluating the composition of inverse functions
👉 Learn how to evaluate an expression with the composition of a function and a function inverse. Just like every other mathematical operation, when given a composition of a trigonometric function and an inverse trigonometric function, you first evaluate the one inside the parenthesis. We
From playlist Evaluate a Composition of Inverse Trigonometric Functions