The Beltrami Identity is a necessary condition for the Euler-Lagrange equation (so if it solves the E-L equation, it solves the Beltrami identity). Here it is derived from the total derivative of the integrand (e.g. Lagrangian).
From playlist Physics

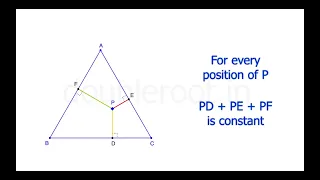
Viviani's Theorem: "Proof" Without Words
Link: https://www.geogebra.org/m/BXUrfwxj
From playlist Geometry: Challenge Problems

C73 Introducing the theorem of Frobenius
The theorem of Frobenius allows us to calculate a solution around a regular singular point.
From playlist Differential Equations
Viviani's Theorem | Visualization and Proof
A visual proof of Viviani's theorem. For any point inside an equilateral triangle, the sum of its perpendicular distances from the three sides is constant. And, this sum is equal to the length of the triangle's altitude. Follow: https://instagram.com/doubleroot.in Music by CeeaDidIt from
From playlist Summer of Math Exposition Youtube Videos

Moving on from Lagrange's equation, I show you how to derive Hamilton's equation.
From playlist Physics ONE

This is a short, animated visual proof of Viviani's theorem, which states that the sum of the distances from any interior point to the sides of an equilateral triangle is equal to the length of the triangle's altitude. #math #geometry #mtbos #manim #animation #theorem #pww #proofwith
From playlist MathShorts

The golden ratio | Lecture 3 | Fibonacci Numbers and the Golden Ratio
The classical definition of the golden ratio. Two positive numbers are said to be in the golden ratio if the ratio between the larger number and the smaller number is the same as the ratio between their sum and the larger number. Phi=(1+sqrt(5))/2 approx 1.618. Join me on Coursera: http
From playlist Fibonacci Numbers and the Golden Ratio

The many facets of complexity of Beltrami fields in Euclidean space - Daniel Peralta-Salas
Workshop on the h-principle and beyond Topic: The many facets of complexity of Beltrami fields in Euclidean space Speaker: Daniel Peralta-Salas Affiliation: Instituto de Ciencias Matemáticas Date: November 02, 2021 Beltrami fields, that is vector fields on $\mathbb R^3$ whose curl is p
From playlist Mathematics

Oily-Maccaroni: A Curious Limit Definition!
Help me create more free content! =) https://www.patreon.com/mathable Merch :v - https://teespring.com/stores/papaflammy https://www.amazon.com/shop/flammablemaths https://shop.spreadshirt.de/papaflammy Become a Member of the Flammily! :0 https:
From playlist Number Theory

Looking at Euler flows through a contact mirror: Universality, Turing… - Eva Miranda
Workshop on the h-principle and beyond Topic: Looking at Euler flows through a contact mirror: Universality, Turing completeness and undecidability Speaker: Eva Miranda Affiliation: Universitat Politècnica de Catalunya Date: November 1, 2021 The dynamics of an inviscid and incompressible
From playlist Mathematics

Wild Weak Solutions to Equations arising in Hydrodynamics - 2/6 - Vlad Vicol
In this course, we will discuss the use of convex integration to construct wild weak solutions in the context of the Euler and Navier-Stokes equations. In particular, we will outline the resolution of Onsager's conjecture as well as the recent proof of non-uniqueness of weak solutions to t
From playlist Hadamard Lectures 2020 - Vlad Vicol and - Wild Weak Solutions to Equations arising in Hydrodynamics

First steps in hyperbolic geometry | Universal Hyperbolic Geometry 4 | NJ Wildberger
This video outlines the basic framework of universal hyperbolic geometry---as the projective study of a circle, or later on the projective study of relativistic geometry. Perpendicularity is defined in terms of duality, the pole-polar correspondence introduced by Apollonius, and we explain
From playlist Universal Hyperbolic Geometry

B24 Introduction to the Bernoulli Equation
The Bernoulli equation follows from a linear equation in standard form.
From playlist Differential Equations

Lecture 18: The Laplace Operator (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858

On the dyadic Hilbert transform – Stefanie Petermichl – ICM2018
Analysis and Operator Algebras Invited Lecture 8.10 On the dyadic Hilbert transform Stefanie Petermichl Abstract: The Hilbert transform is an average of dyadic shift operators. These can be seen as a coefficient shift and multiplier in a Haar wavelet expansion or as a time shifted operat
From playlist Analysis & Operator Algebras

Yilin Wang - 4/4 The Loewner Energy at the Crossroad of Random Conformal Geometry (...)
The Loewner energy for Jordan curves first arises from the large deviations of Schramm-Loewner evolution (SLE), a family of random fractal curves modeling interfaces in 2D statistical mechanics. In a certain way, this energy measures the roundness of a Jordan curve, and we show that it is
From playlist Yilin Wang - The Loewner Energy at the Crossroad of Random Conformal Geometry and Teichmueller Theory

C. Leininger - Teichmüller spaces and pseudo-Anosov homeomorphism (Part 2)
I will start by describing the Teichmuller space of a surface of finite type from the perspective of both hyperbolic and complex structures and the action of the mapping class group on it. Then I will describe Thurston's compactification of Teichmuller space, and state his classification t
From playlist Ecole d'été 2018 - Teichmüller dynamics, mapping class groups and applications

8ECM Invited Lecture: Eva Miranda
From playlist 8ECM Invited Lectures

Cayley-Hamilton Theorem: General Case
Matrix Theory: We state and prove the Cayley-Hamilton Theorem over a general field F. That is, we show each square matrix with entries in F satisfies its characteristic polynomial. We consider the special cases of diagonal and companion matrices before giving the proof.
From playlist Matrix Theory
