
Calculus - The Fundamental Theorem, Part 1
The Fundamental Theorem of Calculus. First video in a short series on the topic. The theorem is stated and two simple examples are worked.
From playlist Calculus - The Fundamental Theorem of Calculus

Images in Math - Pascal's Theorem
This video is about Pascal's Theorem.
From playlist Images in Math

Calculus 5.3 The Fundamental Theorem of Calculus
My notes are available at http://asherbroberts.com/ (so you can write along with me). Calculus: Early Transcendentals 8th Edition by James Stewart
From playlist Calculus

The Abel Prize announcement 2019 - Karen Uhlenbeck
0:48 Introduction by Jim Al-Khalili, British physicist and science communicator 2:38 The Abel Prize announced by Hans Petter Graver, President of The Norwegian Academy of Science and Letters 3:44 Citation by Hans Munthe-Kaas, Chair of the Abel committee 12:06 Popular presentation of the pr
From playlist Karen K. Uhlenbeck

Fourier series + Fourier's theorem
Free ebook http://tinyurl.com/EngMathYT A basic lecture on how to calculate Fourier series and a discussion of Fourier's theorem, which gives conditions under which a Fourier series will converge to a given function.
From playlist Engineering Mathematics

Calculus - The Fundamental Theorem, Part 2
The Fundamental Theorem of Calculus. A discussion of the antiderivative function and how it relates to the area under a graph.
From playlist Calculus - The Fundamental Theorem of Calculus

How to find the position function given the acceleration function
👉 Learn how to approximate the integral of a function using the Reimann sum approximation. Reimann sum is an approximation of the area under a curve or between two curves by dividing it into multiple simple shapes like rectangles and trapezoids. In using the Reimann sum to approximate the
From playlist Riemann Sum Approximation

The Fundamental Theorem of Calculus | Algebraic Calculus One | Wild Egg
In this video we lay out the Fundamental Theorem of Calculus --from the point of view of the Algebraic Calculus. This key result, presented here for the very first time (!), shows how to generalize the Fundamental Formula of the Calculus which we presented a few videos ago, incorporating t
From playlist Algebraic Calculus One

Robert Bryant: Limits, Bubbles, and Singularities: The fundamental ideas of Karen Uhlenbeck
Abstract: Ever since the Greeks, the challenges of understanding limits and infinities have fascinated us, ultimately leading to the development of calculus and much of modern mathematics. When does a limit exist and in what sense? How do we capture these notions in geometric and intuitive
From playlist Abel Lectures

Rellich Kondrachov Theorem for L^2 curvatures in arbitrary dimension- Tristan Rivière
Workshop on Geometric Functionals: Analysis and Applications Topic: Rellich Kondrachov Theorem for L^2 curvatures in arbitrary dimension Speaker: Tristan Rivière Affiliation: ETH Zürich; Member, School of Mathematics Date: March 5, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

Introduction to additive combinatorics lecture 10.8 --- A weak form of Freiman's theorem
In this short video I explain how the proof of Freiman's theorem for subsets of Z differs from the proof given earlier for subsets of F_p^N. The answer is not very much: the main differences are due to the fact that cyclic groups of prime order do not have lots of subgroups, so one has to
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

A. Mondino - Time-like Ricci curvature bounds via optimal transport
Time-like Ricci curvature bounds via optimal transport in Lorentzian synthetic spaces and applications The goal of the talk is to present a recent work in collaboration with Cavalletti (SISSA) on optimal transport in Lorentzian synthetic spaces. The aim is to set up a “Lorentzian analog”
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Jim Al-Khalili: The life and work of Karen Uhlenbeck
Jim Al-Khalili on the life and work of Karen Uhlenbeck. This clip is from the 2019 Abel Prize announcement. You can view the full announcement video here: https://youtu.be/arrl_nM0T4s
From playlist Popular presentations

Jean-Pierre Demailly: Improved bounds for jet differential operators and the Kobayashi conjecture
Abstract: We will discuss several new ideas that can show the existence of jet differential operators on arbitrary projective varieties, and also on general hypersurfaces of ℙn of sufficiently high degree. These results can be applied to improve degree bounds in several hyperbolicity probl
From playlist Algebraic and Complex Geometry
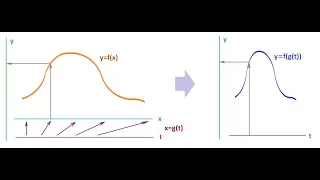
Change of variables and the derivative -- Calculus I
This lecture is on Calculus I. It follows Part I of the book Calculus Illustrated by Peter Saveliev. The text of the book can be found at http://calculus123.com.
From playlist Calculus I
Tight Lower Bounds for 2-query LCCs Over Finite fields - Shubhangi Saraf
Shubhangi Saraf Microsoft Research; Member, School of Mathematics September 27, 2011 A locally correctable code (LCC) is an error correcting code mapping d symbols to n symbols, such that for every codeword c and every received word r that is \delta-close to c, we can recover any coordinat
From playlist Mathematics

Abel Prize Reception in Honor of Karen Uhlenbeck
More videos on http://video.ias.edu
From playlist Related videos on other channels

Alessio Figalli, Fields medallist 2018 - International Meeting - 14 January 2019
https://www.sns.it/it/evento/alessio-figalli-fields-medallist-2018 Alessio Figalli, Fields medallist 2018 International Meeting This event gathers mathematicians that had a major role in Figalli’s career, either by inspiring and guiding him during his early stage, or by collaborating wit
From playlist Centro di Ricerca Matematica Ennio De Giorgi

With Olivia Caramello, André Joyal, Laurent Lafforgue et Alain Connes
From playlist Topos à l'IHES

Math 139 Fourier Analysis Lecture 36: Dirichlet's theorem pt. 3
Proof of the product formula for Dirichlet L-functions. Defining the logarithm of an L-function: technical proposition. Key lemma.
From playlist Course 8: Fourier Analysis