
Maxima and Minima for Quadratic and Cubics | Algebraic Calculus One | Wild Egg
Tangents of algebraic curves are best defined purely algebraically, without recourse to limiting arguments! We apply our techniques for finding such tangents to derive some familiar results for quadratic and cubic polynomial functions and their maxima and minima. We compare also with the c
From playlist Algebraic Calculus One

Algebraic topology: Introduction
This lecture is part of an online course on algebraic topology. This is an introductory lecture, where we give a quick overview of some of the invariants of algebraic topology (homotopy groups, homology groups, K theory, and cobordism). The book "algebraic topology" by Allen Hatcher men
From playlist Algebraic topology

Paul GUNNELLS - Cohomology of arithmetic groups and number theory: geometric, ... 1
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry) and connexion to number theory. The second part will deal with higher rank groups, mainly
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Paul BIRAN - Lagrangian Cobordisms, Dehn-twists and Real Algebraic Geometry
We will explain the relevance of Lagrangian cobordisms in Lefschetz fibrations to the study of the (derived) Fukaya category of the fiber. In particular we will give a cobordism interpretation of Seidel's long exact sequence, introduce cobordism groups and also outline how to study real al
From playlist 2015 Summer School on Moduli Problems in Symplectic Geometry

Cohomology in difference algebra and geometry We view difference algebra as the study of algebraic objects in the topos of difference sets, i.e., as `ordinary algebra’ in a new universe. The methods of topos theory and categorical logic enable us to develop difference homological algebra,
From playlist DART X
A quantitative look at Lagrangian cobordisms - Lisa Traynor
Augmentations and Legendrians at the IAS Topic: A quantitative look at Lagrangian cobordisms Speaker: Lisa Traynor Date: Friday, February 12 Lagrangian cobordisms between Legendrian submanifolds arise in Relative Symplectic Field Theory. In recent years, there has been much progress on an
From playlist Mathematics
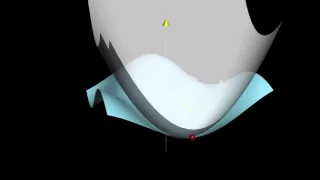
Quadratic approximations of cos(x)sin(y)
From playlist 3d graphs

Aurel PAGE - Cohomology of arithmetic groups and number theory: geometric, ... 2
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry) and connexion to number theory. The second part will deal with higher rank groups, mainly
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

AlgTopReview4: Free abelian groups and non-commutative groups
Free abelian groups play an important role in algebraic topology. These are groups modelled on the additive group of integers Z, and their theory is analogous to the theory of vector spaces. We state the Fundamental Theorem of Finitely Generated Commutative Groups, which says that any such
From playlist Algebraic Topology

Philippe ELBAZ - Cohomology of arithmetic groups and number theory: geometric, ... 3
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry) and connexion to number theory. The second part will deal with higher rank groups, mainly
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Lagrangian cobordisms, enriched knot diagrams, and algebraic invariants - Ipsita Datta
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Lagrangian cobordisms, enriched knot diagrams, and algebraic invariants Speaker: Ipsita Datta Affiliation: Member, School of Mathematics Date: November 4, 2022 We introduce new invariants to the existence of
From playlist Mathematics

Restrictions on the fundamental group of some Lagrangian cobordisms - Chantraine
Restrictions on the fundamental group of some Lagrangian cobordisms Augmentations and Legendrians at the IAS Topic: Restrictions on the fundamental group of some Lagrangian cobordisms Speaker: Baptiste Chantraine Date: Thursday, February 11 In this talk we will describe two methods which
From playlist Mathematics

Yonatan Harpaz - New perspectives in hermitian K-theory II
Warning: around 32:30 in the video, in the slide entitled "Karoubi's conjecture", a small mistake was made - in the third bulleted item the genuine quadratic structure appearing should be the genuine symmetric one (so both the green and red instances of the superscript gq should be gs), an
From playlist New perspectives on K- and L-theory

Yonatan Harpaz - New perspectives in hermitian K-theory I
For questions and discussions of the lecture please go to our discussion forum: https://www.uni-muenster.de/TopologyQA/index.php?qa=k%26l-conference This lecture is part of the event "New perspectives on K- and L-theory", 21-25 September 2020, hosted by Mathematics Münster: https://go.wwu
From playlist New perspectives on K- and L-theory

Philippe ELBAZ - Cohomology of arithmetic groups and number theory: geometric, ... 2
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry) and connexion to number theory. The second part will deal with higher rank groups, mainly
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Classifying (quasi-)smooth varieties up to cobordism - Toni Mikael Annala
Short Talks by Postdoctoral Members Topic: Classifying (quasi-)smooth varieties up to cobordism Speaker: Toni Mikael Annala Affiliation: Member, School of Mathematics Date: September 20, 2022
From playlist Mathematics

A Controlled Mather Thurston Theorem - Mike Freedman
Workshop on the h-principle and beyond Topic: A Controlled Mather Thurston Theorem Speaker: Mike Freedman Affiliation: Microsoft Date: November 03, 2021 Abstract: The "c-principle" is a cousin of Gromov's h-principle in which cobordism rather than homotopy is required to (canonically) s
From playlist Mathematics

Lagrangian Cobordisms and Enriched Knot Diagrams - Ipsita Datta
Joint IAS/Princeton University Symplectic Geometry Seminar Topic: Lagrangian Cobordisms and Enriched Knot Diagrams Speaker: Ipsita Datta Affiliation: Member, School of Mathematics Date: November 08, 2021 We present some obstructions to the existence of Lagrangian cobordisms in ℝ4. The ob
From playlist Mathematics

Khovanov Homology and Virtual Knot Cobordism by Louis H. Kauffman
PROGRAM KNOTS THROUGH WEB (ONLINE) ORGANIZERS: Rama Mishra, Madeti Prabhakar, and Mahender Singh DATE & TIME: 24 August 2020 to 28 August 2020 VENUE: Online Due to the ongoing COVID-19 pandemic, the original program has been canceled. However, the meeting will be conducted through onl
From playlist Knots Through Web (Online)

In this first video on cosets, I show you the equivalence relation on a group, G, that will turn out to create equivalence classes, which are actually cosets. We will prove later that these equivalence classes created by an element in the group, G, are equal to the set of element made up
From playlist Abstract algebra