
R - Structural Equation Model Basics Lecture 1
Lecturer: Dr. Erin M. Buchanan Missouri State University Summer 2016 This lecture covers the basic terminology for structural equation modeling including: identification, scaling, variable types, manifest/latent variables, path coefficient types, endogenous/exogenous variables, degrees o
From playlist Structural Equation Modeling

An Introduction to Abstract Data Types ADT Data Structures Source Code: https://github.com/williamfiset/algorithms My website: http://www.williamfiset.com =================================== Practicing for interviews? I have used, and recommend `Cracking the Coding Interview` which go
From playlist Data structures playlist

R - Latent Growth (Curve) Example
Lecturer: Dr. Erin M. Buchanan Missouri State University Summer 2016 This video covers an example of how to perform a latent growth model with steps over intercepts, random intercepts, random slopes, slopes, covariance, and residuals. Lavaan and the growth() functions are used. Lecture
From playlist Structural Equation Modeling

Model Theory - part 08 - Syntactic Catgories
These are the categories where functors from these dudes are models... these take forever to define. On top of it, these end up just being friggin' definable sets and definable morphisms!! I remember being a place in here where there is a diagram which i say commutes but I need to actually
From playlist Model Theory

MOR_012 - Linguistic Micro-Lectures: Affixes
What are affixes and how can they be defined and represented? Within less than two minutes Prof. Handke explains the main principles of affixation using examples from PDE and other languages.
From playlist Micro-Lectures - Morphology

Monica Vazirani: Representations of the affine BMW category
The BMW algebra is a deformation of the Brauer algebra, and has the Hecke algebra of type A as a quotient. Its specializations play a role in types B, C, D akin to that of the symmetric group in Schur-Weyl duality. I will discuss Walker’s TQFT-motivated 1-handle construction of a family of
From playlist Workshop: Monoidal and 2-categories in representation theory and categorification

Data Structures: List as abstract data type
See complete series of videos in data structures here: http://www.youtube.com/playlist?list=PL2_aWCzGMAwI3W_JlcBbtYTwiQSsOTa6P&feature=view_all In this lesson, we will introduce a dynamic list structure as an abstract data type and then see one possible implementation of dynamic list using
From playlist Data structures

David Rydh. Local structure of algebraic stacks and applications
Abstract: Some natural moduli problems, such as moduli of sheaves and moduli of singular curves, give rise to stacks with infinite stabilizers that are not known to be quotient stacks. The local structure theorem states that many stacks locally look like the quotient of a scheme by the act
From playlist CORONA GS

Martin Larsson: Affine Volterra processes and models for rough volatility
Abstract: Motivated by recent advances in rough volatility modeling, we introduce affine Volterra processes, defined as solutions of certain stochastic convolution equations with affine coefficients. Classical affine diffusions constitute a special case, but affine Volterra processes are n
From playlist Probability and Statistics
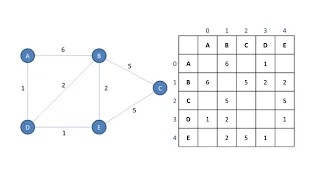
Graph Data Structure 1. Terminology and Representation (algorithms)
This is the first in a series of videos about the graph data structure. It mentions the applications of graphs, defines various terminology associated with graphs, and describes how a graph can be represented programmatically by means of adjacency lists or an adjacency matrix.
From playlist Data Structures

Rod Gover - Geometric Compactification, Cartan holonomy, and asymptotics
Conformal compactification has long been recognised as an effective geometric framework for relating conformal geometry, and associated field theories « at infinity », to the asymptotic phenomena of an interior (pseudo‐)‐Riemannian geometry of one higher dimension. It provides an effective
From playlist Ecole d'été 2014 - Analyse asymptotique en relativité générale

Introduction to Elliptic Curves 1 by Anupam Saikia
PROGRAM : ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (ONLINE) ORGANIZERS : Ashay Burungale (California Institute of Technology, USA), Haruzo Hida (University of California, Los Angeles, USA), Somnath Jha (IIT - Kanpur, India) and Ye Tian (Chinese Academy of Sciences, China) DA
From playlist Elliptic Curves and the Special Values of L-functions (ONLINE)
Latent Growth Curve Modeling | Part 1
In the second installment of this video series, I will discuss the essential concepts in Growth Curve Modeling.
From playlist Growth Curve Models

Dynamics on character varieties - William Goldman
Character Varieties, Dynamics and Arithmetic Topic: Dynamics on character varieties Speaker: William Goldman Affiliation: University of Maryland; Member, School of Mathematics Date: November 17, 2021 In these two talks, I will describe how the classification of locally homogeneous geomet
From playlist Mathematics

Holomorphic rigid geometric structures on compact manifolds by Sorin Dumitrescu
Higgs bundles URL: http://www.icts.res.in/program/hb2016 DATES: Monday 21 Mar, 2016 - Friday 01 Apr, 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore DESCRIPTION: Higgs bundles arise as solutions to noncompact analog of the Yang-Mills equation. Hitchin showed that irreducible solutio
From playlist Higgs Bundles

Gianni De Fabritiis: "Machine Learning for Drug Design"
Machine Learning for Physics and the Physics of Learning Tutorials 2019 "Machine Learning for Drug Design" Gianni De Fabritiis, Universitat Pompeu Fabra Institute for Pure and Applied Mathematics, UCLA September 6, 2019 For more information: http://www.ipam.ucla.edu/programs/workshops/m
From playlist Machine Learning for Physics and the Physics of Learning 2019

Bruno Correia - Exploring new molecular representations for the design of biological function
Recorded 26 January 2023. Bruno Correia of the École Polytechnique Fédérale de Lausanne presents "Exploring new molecular representations for the design of biological function" at IPAM's Learning and Emergence in Molecular Systems Workshop. Abstract: Finely orchestrated protein activities
From playlist 2023 Learning and Emergence in Molecular Systems

Chemistry 107. Inorganic Chemistry. Lecture 16
UCI Chemistry: Inorganic Chemistry (Fall 2014) Lec 16. Inorganic Chemistry -- Nature of the Adduct View the complete course: http://ocw.uci.edu/courses/chem_107_inorganic_chemistry.html Instructor: Matthew D. Law License: Creative Commons CC-BY-SA Terms of Use: http://ocw.uci.edu/info Mor
From playlist Chem 107: Week 6

A stacky approach to crystalline (and prismatic) cohomology - Vladimir Drinfeld
Joint IAS/Princeton University Number Theory Seminar Topic: A stacky approach to crystalline (and prismatic) cohomology Speaker: Vladimir Drinfeld Affiliation: The University of Chicago; Visiting Professor, School of Mathematics Date: October 3, 2019 For more video please visit http://vi
From playlist Mathematics

R - Latent Growth Models Lecture
Lecturer: Dr. Erin M. Buchanan Spring 2021 https://www.patreon.com/statisticsofdoom In this section, you will learn about latent growth models and how to analyze them in a similar fashion to multilevel models. You can learn more at: https://statisticsofdoom.com/page/structural-equation
From playlist Structural Equation Modeling 2020