
Computational Aspects in the Braid Group and Applications to Cryptography - Mina Teicher
Mina Teicher Bar-Ilan University; Member, School of Mathematics March 12, 2012 The braid group on n strands may be viewed as an infinite analog of the symmetric group on n elements with additional topological phenomena. It appears in several areas of mathematics, physics and computer scien
From playlist Mathematics

Symmetric Groups (Abstract Algebra)
Symmetric groups are some of the most essential types of finite groups. A symmetric group is the group of permutations on a set. The group of permutations on a set of n-elements is denoted S_n. Symmetric groups capture the history of abstract algebra, provide a wide range of examples in
From playlist Abstract Algebra

Bert Wiest: Pseudo-Anosov braids are generic
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Geometry

Cyclic Groups (Abstract Algebra)
Cyclic groups are the building blocks of abelian groups. There are finite and infinite cyclic groups. In this video we will define cyclic groups, give a list of all cyclic groups, talk about the name “cyclic,” and see why they are so essential in abstract algebra. Be sure to subscribe s
From playlist Abstract Algebra

Group Definition (expanded) - Abstract Algebra
The group is the most fundamental object you will study in abstract algebra. Groups generalize a wide variety of mathematical sets: the integers, symmetries of shapes, modular arithmetic, NxM matrices, and much more. After learning about groups in detail, you will then be ready to contin
From playlist Abstract Algebra

The affine Hecke category is a monoidal colimit - James Tao
Geometric and Modular Representation Theory Seminar Topic: The affine Hecke category is a monoidal colimit Speaker: James Tao Affiliation: Massachusetts Institute of Technology Date: February 24, 2021 For more video please visit http://video.ias.edu
From playlist Seminar on Geometric and Modular Representation Theory

Dihedral Group (Abstract Algebra)
The Dihedral Group is a classic finite group from abstract algebra. It is a non abelian groups (non commutative), and it is the group of symmetries of a regular polygon. This group is easy to work with computationally, and provides a great example of one connection between groups and geo
From playlist Abstract Algebra

Path isomorphisms between quiver Hecke and diagrammatic Bott-Samelson endomorphism... - Amit Hazi
Virtual Workshop on Recent Developments in Geometric Representation Theory Topic: Path isomorphisms between quiver Hecke and diagrammatic Bott-Samelson endomorphism algebras Speaker: Amit Hazi Affiliation: University of London Date: November 17, 2020 For more video please visit http://vi
From playlist Virtual Workshop on Recent Developments in Geometric Representation Theory

Geordie Williamson: Langlands and Bezrukavnikov II Lecture 20
SMRI Seminar Series: 'Langlands correspondence and Bezrukavnikov’s equivalence' Geordie Williamson (University of Sydney) Abstract: The second part of the course focuses on affine Hecke algebras and their categorifications. Last year I discussed the local Langlands correspondence in bro
From playlist Geordie Williamson: Langlands correspondence and Bezrukavnikov’s equivalence

algebraic geometry 5 Affine space and the Zariski topology
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It covers the definition of affine space and its Zariski topology.
From playlist Algebraic geometry I: Varieties

Alexei Davydov: Condensation of anyons in topological states of matter & structure theory
Condensation of anyons in topological states of matter and structure theory of E_2-algebras Abstract: The talk will be on the algebraic structure present in both parts of the title. This algebraic story is most pronounced for E2-algebras in the category of 2-vector spaces (also known as b
From playlist SMRI Seminars
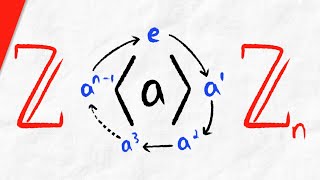
Cyclic Groups, Generators, and Cyclic Subgroups | Abstract Algebra
We introduce cyclic groups, generators of cyclic groups, and cyclic subgroups. We discuss an isomorphism from finite cyclic groups to the integers mod n, as well as an isomorphism from infinite cyclic groups to the integers. We establish a cyclic group of order n is isomorphic to Zn, and a
From playlist Abstract Algebra

Geordie Williamson: Langlands and Bezrukavnikov II Lecture 19
SMRI Seminar Series: 'Langlands correspondence and Bezrukavnikov’s equivalence' Geordie Williamson (University of Sydney) Abstract: The second part of the course focuses on affine Hecke algebras and their categorifications. Last year I discussed the local Langlands correspondence in bro
From playlist Geordie Williamson: Langlands correspondence and Bezrukavnikov’s equivalence

David Jordan: Skeins, clusters, and character sheaves
Abstract: Skein algebras are certain diagrammatically defined algebras spanned by tangles drawn on the cylinder of a surface, with multiplication given by stacking diagrams. Quantum cluster algebras are certain systems of mutually birational quantum tori whose defining relations are encode
From playlist Algebraic and Complex Geometry
Branimir Cacic, Classical gauge theory on quantum principalbundles
Noncommutative Geometry Seminar (Europe), 20 October 2021
From playlist Global Noncommutative Geometry Seminar (Europe)

algebraic geometry 17 Affine and projective varieties
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It covers the relation between affine and projective varieties, with some examples such as a cubic curve and the twisted cubic.
From playlist Algebraic geometry I: Varieties

Knot Categorification From Mirror Symmetry (Lecture- 1) by Mina Aganagic
PROGRAM QUANTUM FIELDS, GEOMETRY AND REPRESENTATION THEORY 2021 (ONLINE) ORGANIZERS: Aswin Balasubramanian (Rutgers University, USA), Indranil Biswas (TIFR, india), Jacques Distler (The University of Texas at Austin, USA), Chris Elliott (University of Massachusetts, USA) and Pranav Pan
From playlist Quantum Fields, Geometry and Representation Theory 2021 (ONLINE)

Maria Chlouveraki, Research talk - 29 January 2015
Maria Chlouveraki (Université de Versailles - St Quentin) - Research talk http://www.crm.sns.it/course/4206/ Yokonuma-Hecke algebras were introduced by Yokonuma in the 60's as generalisations of Iwahori-Hecke algebras. They have recently attracted the interest of topologists, because the
From playlist Lie Theory and Representation Theory - 2015

Affine Springer fibers and representation theory - Cheng-Chiang Tsai
Short talk by postdoctoral members Topic: Affine Springer fibers and representation theory Speaker: Cheng-Chiang Tsai, Member, School of Mathematics For more videos, visit http://video.ias.edu
From playlist Mathematics
