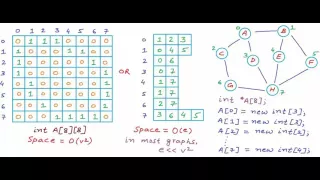
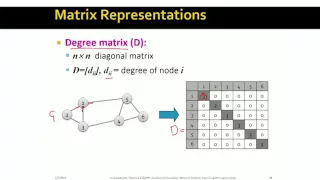
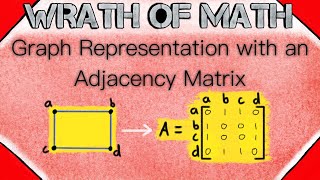
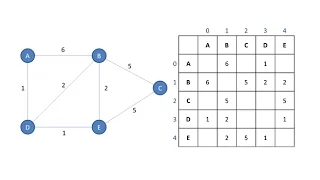
Adjacency list
In graph theory and computer science, an adjacency list is a collection of unordered lists used to represent a finite graph. Each unordered list within an adjacency list describes the set of neighbors of a particular vertex in the graph. This is one of several commonly used representations of graphs for use in computer programs. (Wikipedia).