Noise (electronics) | Time series models
Additive white Gaussian noise
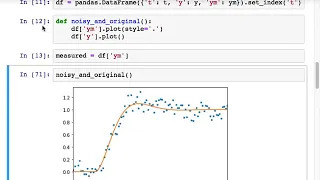
Additive white Gaussian noise (AWGN) is a basic noise model used in information theory to mimic the effect of many random processes that occur in nature. The modifiers denote specific characteristics: * Additive because it is added to any noise that might be intrinsic to the information system. * White refers to the idea that it has uniform power across the frequency band for the information system. It is an analogy to the color white which has uniform emissions at all frequencies in the visible spectrum. * Gaussian because it has a normal distribution in the time domain with an average time domain value of zero. Wideband noise comes from many natural noise sources, such as the thermal vibrations of atoms in conductors (referred to as thermal noise or Johnson–Nyquist noise), shot noise, black-body radiation from the earth and other warm objects, and from celestial sources such as the Sun. The central limit theorem of probability theory indicates that the summation of many random processes will tend to have distribution called Gaussian or Normal. AWGN is often used as a channel model in which the only impairment to communication is a linear addition of wideband or white noise with a constant spectral density (expressed as watts per hertz of bandwidth) and a Gaussian distribution of amplitude. The model does not account for fading, frequency selectivity, interference, nonlinearity or dispersion. However, it produces simple and tractable mathematical models which are useful for gaining insight into the underlying behavior of a system before these other phenomena are considered. The AWGN channel is a good model for many satellite and deep space communication links. It is not a good model for most terrestrial links because of multipath, terrain blocking, interference, etc. However, for terrestrial path modeling, AWGN is commonly used to simulate background noise of the channel under study, in addition to multipath, terrain blocking, interference, ground clutter and self interference that modern radio systems encounter in terrestrial operation. (Wikipedia).