Additive disequilibrium and z statistic

Statistical inference

Additive disequilibrium (D) is a statistic that estimates the difference between observed genotypic frequencies and the genotypic frequencies that would be expected under Hardy–Weinberg equilibrium. At a biallelic locus with alleles 1 and 2, the additive disequilibrium exists according to the equations where fij is the frequency of genotype ij in the population, p is the allele frequency in the population, and D is the additive disequilibrium coefficient. Having a value of D > 0 indicates an excess of homozygotes/deficiency of heterozygotes in the population, whereas D < 0 indicates an excess of heterozygotes/deficiency of homozygotes. When D = 0, the genotypes are considered to be in Hardy Weinberg Equilibrium. In practice, the estimated additive disequilibrium from a sample, , will rarely be exactly 0, but it may be small enough to conclude that it is not significantly different from 0. Finding the value of the additive disequilibrium coefficient provides an alternative assessment in accepting or rejecting Hardy Weinberg Equilibrium in a set of genotypic frequencies. Because the genotype and allele frequencies must be positive numbers in the interval (0,1), there exists a constraint on the range of possible values for D, which is as follows: To estimate D from a sample, use the formula: where n11 (n12) is the number of individuals in the sample with that particular genotype and n is the total number of individuals in the sample. Note that and are sample estimates of the population genotype and allele frequencies. The approximate sampling variance of (given by ) is: From this an estimated 95% confidence interval can be calculated, which is Note: is also equal to the estimated standard deviation . If the confidence interval for does not include zero, we can reject the null hypothesis for Hardy Weinberg Equilibrium. * Similarly, we can also test for Hardy Weinberg Equilibrium using the z-statistic, which uses information from the estimate of additive disequilibrium to determine significance. When using the z-statistic, however, the goal is to transform the statistic in a way such that asymptotically, it has a standard normal distribution. To do this, divide by its standard deviation, which gives the simplified equation: When z is large, and thus the departure from Hardy Weinberg Equilibrium are also large. If the value of z is sufficiently large, it is unlikely that the deviations would occur by chance and thus the hypothesis of Hardy Weinberg Equilibrium can be rejected. To determine if z is significantly larger or smaller than expected under Hardy Weinberg Equilibrium, find "the probability of observing" a value as or more extreme as the observed z "under the null hypothesis". The tail probability is normally used, (y > z), where y is standard normal random variable. When z is positive, the tail probability is 1 − (y ≤ z). Because normal distributions are symmetric, the upper and lower tail probabilities will be equal, and thus you can find the upper probability and multiply by 2 to find the combined tail probabilities. If z is negative, find the negative tail probability, (y ≤ z), and multiply by 2 to find the combined probability in both upper and lower tails. The probability values calculated from these equations can be analyzed by comparison to a pre-specified value of α. When the observed probability p ≤ α, we can "reject the null hypothesis of Hardy Weinberg Equilibrium". If p > α, we fail to reject the null hypothesis. Commonly used values of α are 0.05, 0.01, and 0.001. At a significance of α = 0.05, we can reject the hypothesis of Hardy Weinberg Equilibrium if the absolute value of z is "greater than or equal to the critical value 1.96" for the two-sided test. (Wikipedia).

Find x given the z-score, sample mean, and sample standard deviation

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Find x given the z-score, sample mean, and sample standard deviation

From playlist Statistics

Lecture06 Standard Deviation

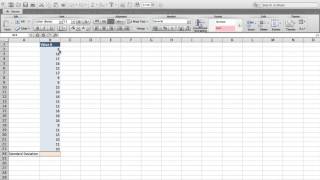
The dispersion of data by means of the standard deviation.

From playlist Medical Statistics

Inverse normal with Z Table

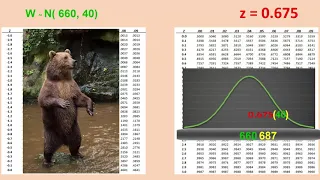
Determining values of a variable at a particular percentile in a normal distribution

From playlist Unit 2: Normal Distributions

Definition of a Z-Score

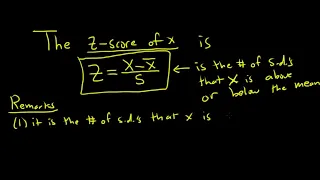
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Z-Score

From playlist Statistics

Computing z-scores(standard scores) and comparing them

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Computing z-scores(standard scores) and comparing them

From playlist Statistics

Univariate and Multivariate selection by Bruce Walsh

Second Bangalore School on Population Genetics and Evolution URL: http://www.icts.res.in/program/popgen2016 DESCRIPTION: Just as evolution is central to our understanding of biology, population genetics theory provides the basic framework to comprehend evolutionary processes. Population

From playlist Second Bangalore School on Population Genetics and Evolution

Chiara Sabatti: Knockoff genotypes: value in counterfeit

CIRM VIRTUAL EVENT Recorded during the meeting "Mathematical Methods of Modern Statistics 2" the June 05, 2020 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians

From playlist Virtual Conference

Excel Statistical Analysis 14: Z-Score, Empirical Rule , Chebyshev Theorem: # of Standard Deviations

Download Excel File: https://excelisfun.net/files/Ch03-ESA.xlsm Learn about the z-score (number of standard deviations) and how to calculate it and use it in the Empirical Rule and Chebyshev's Theorem. Topics: 1. (00:00) Introduction to Z-Score 2. (01:23) Basics of Z-Score Calculations usi

From playlist Excel Statistical Analysis for Business Class Playlist of Videos from excelisfun

Multilocus genetics by Kavita Jain

Winter School on Quantitative Systems Biology DATE:04 December 2017 to 22 December 2017 VENUE:Ramanujan Lecture Hall, ICTS, Bengaluru The International Centre for Theoretical Sciences (ICTS) and the Abdus Salam International Centre for Theoretical Physics (ICTP), are organizing a Winter S

From playlist Winter School on Quantitative Systems Biology

ICTS Special Colloquium by Wolfgang Stephan

From playlist Second Bangalore School on Population Genetics and Evolution

Ruth Heller: Optimal control of false discovery criteria in the general two-group model

CIRM VIRTUAL EVENT Recorded during the meeting "Mathematical Methods of Modern Statistics 2" the June 03, 2020 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians

From playlist Virtual Conference

Normal Distribution: Z-Scores

This lesson explains how to determine a z-score and how to find a z-score for a given data value. The percent of data above and below a data value and z-score is also found. Site: http://mathispower4u.com

From playlist The Normal Distribution

Alison Etheridge & Nick Barton: Applying the infinitesimal model

The infinitesimal model is based on the assumption that, conditional on the pedigree, the joint distribution of trait values is multivariate normal, then, selecting parents does not alter the variance amongst offspring. We explain how the infinitesimal model extends to include dominance as

From playlist Probability and Statistics

Understanding z-scores(standard scores) as a measure of relative standing

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Understanding z-scores(standard scores) as a measure of relative standing. Given several z-scores, the sample mean, and the sample standard deviation, we find the values of x both with the formula and intuitively.

From playlist Statistics

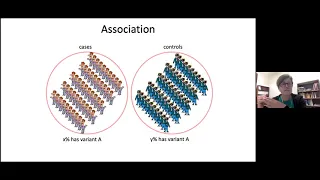
Nicola Armstrong - Genome-Wide Association Studies and beyond

Associate Professor Nicola Armstrong (Murdoch University) presents “Genome-Wide Association Studies and beyond”, 22 October 2020 (seminar organised by ANU).

From playlist Statistics Across Campuses

An example of z scores for proportions.

z scores, statistics, p values Like us on: http://www.facebook.com/PartyMoreStudyLess

From playlist z scores

Introduction to mutation, selection and drift by Bruce Walsh

From playlist Second Bangalore School on Population Genetics and Evolution

Using structure to select features in high dimension. - Azencott - Workshop 3 - CEB T1 2019

Chloé-Agathe Azencott (Mines-Paristech) / 02.04.2019 Using structure to select features in high dimension. Many problems in genomics require the ability to identify relevant features in data sets containing many more orders of magnitude than samples. This setup poses different statistic

From playlist 2019 - T1 - The Mathematics of Imaging

Standard Normal Distribution of Z Scores

Z-scores called standardized scores are normally distributed

From playlist Unit 2: Normal Distributions

Molecular evolution (1), introduction.

This video revisits some of the concepts from the previous lectures about population genetics from a perspective in which the alleles are defined as specific changes to the DNA nucleotides rather than abstract differences between alleles. Some new topics are also introduced. Topics describ

From playlist TAMU: Bio 312 - Evolution | CosmoLearning Biology

Additive disequilibrium and z statistic

Related pages