
Matrix Limits and Markov Chains
In this video I present a cool application of linear algebra in which I use diagonalization to calculate the eventual outcome of a mixing problem. This process is a simple example of what's called a Markov chain. Note: I just got a new tripod and am still experimenting with it; sorry if t
From playlist Eigenvalues

(ML 14.3) Markov chains (discrete-time) (part 2)
Definition of a (discrete-time) Markov chain, and two simple examples (random walk on the integers, and a oversimplified weather model). Examples of generalizations to continuous-time and/or continuous-space. Motivation for the hidden Markov model.
From playlist Machine Learning

Prob & Stats - Markov Chains (8 of 38) What is a Stochastic Matrix?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is a stochastic matrix. Next video in the Markov Chains series: http://youtu.be/YMUwWV1IGdk
From playlist iLecturesOnline: Probability & Stats 3: Markov Chains & Stochastic Processes

Prob & Stats - Markov Chains (10 of 38) Regular Markov Chain
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is a regular Markov chain. Next video in the Markov Chains series: http://youtu.be/DeG8MlORxRA
From playlist iLecturesOnline: Probability & Stats 3: Markov Chains & Stochastic Processes

(ML 18.4) Examples of Markov chains with various properties (part 1)
A very simple example of a Markov chain with two states, to illustrate the concepts of irreducibility, aperiodicity, and stationary distributions.
From playlist Machine Learning

Dana Randall: Sampling algorithms and phase transitions
Markov chain Monte Carlo methods have become ubiquitous across science and engineering to model dynamics and explore large combinatorial sets. Over the last 20 years there have been tremendous advances in the design and analysis of efficient sampling algorithms for this purpose. One of the
From playlist Probability and Statistics
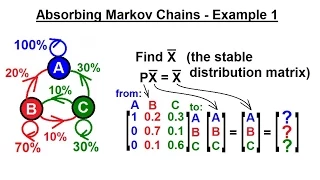
Prob & Stats - Markov Chains (21 of 38) Absorbing Markov Chains - Example 1
Visit http://ilectureonline.com for more math and science lectures! In this video I will find the stable distribution matrix in an absorbing Markov chain. Next video in the Markov Chains series: http://youtu.be/1bErNmzD8Sw
From playlist iLecturesOnline: Probability & Stats 3: Markov Chains & Stochastic Processes

Prob & Stats - Markov Chains: Method 2 (35 of 38) Finding the Stable State & Transition Matrices
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain the standard form of the absorbing Markov chain. Next video in the Markov Chains series: http://youtu.be/MrmMyK5CuWs
From playlist iLecturesOnline: Probability & Stats 3: Markov Chains & Stochastic Processes

“Choice Modeling and Assortment Optimization” - Session II - Prof. Huseyin Topaloglu
This module overviews static and dynamic assortment optimization problems. We will start with an introduction to discrete choice modeling and discuss estimation issues when fitting a choice model to observed sales histories. Following this introduction, we will discuss static and dynamic a
From playlist Thematic Program on Stochastic Modeling: A Focus on Pricing & Revenue Management

Natural Language Processing (Part 6): Text Generation with Markov Chains in Python
This six-part video series goes through an end-to-end Natural Language Processing (NLP) project in Python to compare stand up comedy routines. - Natural Language Processing (Part 1): Introduction to NLP & Data Science - Natural Language Processing (Part 2): Data Cleaning & Text Pre-Proces
From playlist NLP Series

Probability on Kazhdan Groups (Lecture 1) by Gábor Pete
PROGRAM: PROBABILISTIC METHODS IN NEGATIVE CURVATURE ORGANIZERS: Riddhipratim Basu (ICTS - TIFR, India), Anish Ghosh (TIFR, Mumbai, India), Subhajit Goswami (TIFR, Mumbai, India) and Mahan M J (TIFR, Mumbai, India) DATE & TIME: 27 February 2023 to 10 March 2023 VENUE: Madhava Lecture Hall
From playlist PROBABILISTIC METHODS IN NEGATIVE CURVATURE - 2023
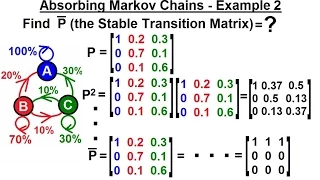
Prob & Stats - Markov Chains (22 of 38) Absorbing Markov Chains - Example 2
Visit http://ilectureonline.com for more math and science lectures! In this video I will find the stable transition matrix in an absorbing Markov chain. Next video in the Markov Chains series: http://youtu.be/hMceS_HIcKY
From playlist iLecturesOnline: Probability & Stats 3: Markov Chains & Stochastic Processes

Sylvia Frühwirth-Schnatter: Bayesian econometrics in the Big Data Era
Abstract: Data mining methods based on finite mixture models are quite common in many areas of applied science, such as marketing, to segment data and to identify subgroups with specific features. Recent work shows that these methods are also useful in micro econometrics to analyze the beh
From playlist Probability and Statistics

Regularized Functional Inequalities and Applications to Markov Chains by Pierre Youssef
PROGRAM: TOPICS IN HIGH DIMENSIONAL PROBABILITY ORGANIZERS: Anirban Basak (ICTS-TIFR, India) and Riddhipratim Basu (ICTS-TIFR, India) DATE & TIME: 02 January 2023 to 13 January 2023 VENUE: Ramanujan Lecture Hall This program will focus on several interconnected themes in modern probab
From playlist TOPICS IN HIGH DIMENSIONAL PROBABILITY

Experimentation with Temporal Interference: by Peter W Glynn
PROGRAM: ADVANCES IN APPLIED PROBABILITY ORGANIZERS: Vivek Borkar, Sandeep Juneja, Kavita Ramanan, Devavrat Shah, and Piyush Srivastava DATE & TIME: 05 August 2019 to 17 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Applied probability has seen a revolutionary growth in resear
From playlist Advances in Applied Probability 2019

L25.7 Steady-State Probabilities and Convergence
MIT RES.6-012 Introduction to Probability, Spring 2018 View the complete course: https://ocw.mit.edu/RES-6-012S18 Instructor: Patrick Jaillet License: Creative Commons BY-NC-SA More information at https://ocw.mit.edu/terms More courses at https://ocw.mit.edu
From playlist MIT RES.6-012 Introduction to Probability, Spring 2018

From playlist Contributed talks One World Symposium 2020

Nexus Trimester - Raymond Yeung (The Chinese University of Hong Kong) 1/3
Shannon's Information Measures and Markov Structures Raymond Yeung (The Chinese University of Hong Kong) February 18,2016 Abstract: Most studies of finite Markov random fields assume that the underlying probability mass function (pmf) of the random variables is strictly positive. With thi
From playlist Nexus Trimester - 2016 - Fundamental Inequalities and Lower Bounds Theme

Integrating Inference with Stochastic Process Algebra Models - Jane Hillston, Edinburgh
ProPPA is a probabilistic programming language for continuous-time dynamical systems, developed as an extension of the stochastic process algebra Bio-PEPA. It offers a high-level syntax for describing systems of interacting components with stochastic behaviours where some of the parameters
From playlist Logic and learning workshop

Prob & Stats - Markov Chains (20 of 38) Absorbing Markov Chains - Definition 2
Visit http://ilectureonline.com for more math and science lectures! In this video I will define the absorbing Markov in a nxn matrix and 3x3 matrix. Next video in the Markov Chains series: http://youtu.be/cZKAVOEWcrg
From playlist iLecturesOnline: Probability & Stats 3: Markov Chains & Stochastic Processes