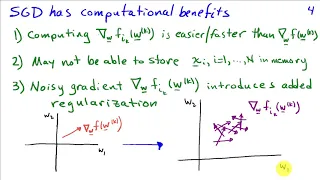
Optimization algorithms and methods
Adaptive coordinate descent
Adaptive coordinate descent is an improvement of the coordinate descent algorithm to non-separable optimization by the use of . The adaptive coordinate descent approach gradually builds a transformation of the coordinate system such that the new coordinates are as decorrelated as possible with respect to the objective function. The adaptive coordinate descent was shown to be competitive to the state-of-the-art evolutionary algorithms and has the following invariance properties: 1. * Invariance with respect to monotonous transformations of the function (scaling) 2. * Invariance with respect to orthogonal transformations of the search space (rotation). CMA-like Adaptive Encoding Update (b) mostly based on principal component analysis (a) is used to extend the coordinate descent method (c) to the optimization of non-separable problems (d). The adaptation of an appropriate coordinate system allows adaptive coordinate descent to outperform coordinate descent on non-separable functions. The following figure illustrates the convergence of both algorithms on 2-dimensional Rosenbrock function up to a target function value , starting from the initial point . The adaptive coordinate descent method reaches the target value after only 325 function evaluations (about 70 times faster than coordinate descent), that is comparable to gradient-based methods. The algorithm has linear time complexity if update coordinate system every D iterations, it is also suitable for large-scale (D>>100) non-linear optimization. (Wikipedia).