
This is part of a series of lectures on the Zermelo-Fraenkel axioms for set theory. We discuss the axiom of foundation, which says that the membership relation is well founded, and give some examples of the bizarre things that can happen if sets are allowed to be non-well-founded. For
From playlist Zermelo Fraenkel axioms

This lecture is part of an online course on the Zermelo Fraenkel axioms of set theory. This lecture gives an overview of the axioms, describes the von Neumann hierarchy, and sketches several approaches to interpreting the axioms (Platonism, von Neumann hierarchy, multiverse, formalism, pra
From playlist Zermelo Fraenkel axioms

Mark Bickford: Constructive Set Theory in Nuprl Type Theory
The lecture was held within the framework of the Hausdorff Trimester Program: Constructive Mathematics. Abstract: Aczel propsed CZF as a foundation for constructive mathematics and gave an interpretation of it in Martin-Löf type theory. He then extended the theory with the Regular Extens
From playlist Workshop: "Constructive Mathematics"

Axioms of Constructive Set Theory Explained
In this video we're going to discuss the various axiom schemes of constructive set theories and how they relate to type theory. I cover BCST, ECST, IKP, KPI, KP, CST, CZF, IZF, Mac Lane, Z and variants equi-consistent to ETCS from category theory, and then of course ZF and ZFC. The text I
From playlist Logic

What's so wrong with the Axiom of Choice ?
One of the Zermelo- Fraenkel axioms, called axiom of choice, is remarkably controversial. It links to linear algebra and several paradoxes- find out what is so strange about it ! (00:22) - Math objects as sets (00:54) - What axioms we use ? (01:30) - Understanding axiom of choice (03:2
From playlist Something you did not know...

My notes are available at http://asherbroberts.com/ (so you can write along with me). Calculus: Early Transcendentals 8th Edition by James Stewart
From playlist Calculus

Isomorphic Structures of any Kind are `Equal' in HoTT: But What... Structure? - Peter Aczel
Peter Aczel The Unviersity of Manchester; Member,School of Mathematics February 7, 2013 For more videos, visit http://video.ias.edu
From playlist Mathematics

This is part of a series of lectures on the Zermelo-Fraenkel axioms for set theory. We dicuss the axiom of chice, and sketch why it is independent of the other axioms of set theory. For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj52EKVgPi-p50f
From playlist Zermelo Fraenkel axioms

The Simplest Math No One Can Agree on- A Paradox of Choice
To build our mathematics we need a starting point, rules to dictate what we can do and assumed basic truths to serve as a foundation as we seek understanding of higher level problems. But what happens when we can't agree on what we should start with?
From playlist Summer of Math Exposition Youtube Videos

The antiderivative derivative club
You may have been told that derivatives and anti derivatives are inverse operations, but in this video I show that it is not quite true (because of the constants), but I show that one can actually define “super” derivatives and “super” antiderivatives so that they actually become inverses
From playlist Calculus

How do we handle the fact that there are many antiderivatives? - Week 10 - Lecture 1 - Mooculus
Subscribe at http://www.youtube.com/kisonecat
From playlist Ohio State: Jim Fowler's Calculus One Lectures | CosmoLearning Mathematics

Furio Honsell - Tribute to Ennio De Giorgi - 20 September 2016
Honsell, Furio "Implementing Cantor’s paradise in constructive type theory"
From playlist A Mathematical Tribute to Ennio De Giorgi
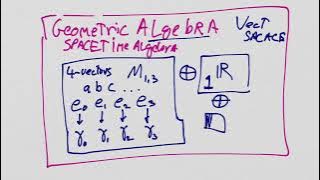
QED Prerequisites Geometric Algebra 3: The symmetric part
In this lesson we begin unpealing the spacetime product of two 4-vectors. The spacetime product can be split into a symmetric and anti-symmetric part and it is critical to understand what each of these two parts represents. We begin with the symmetric part. lease consider supporting thi
From playlist QED- Prerequisite Topics

The Illusion of Certainty: Risk, Probability, and Chance
Stuff happens. The weather forecast says it’s sunny, but you just got drenched. You got a flu shot—but you’re sick in bed with the flu. Your best friend from Boston met your other best friend from San Francisco. Coincidentally. What are the odds? Risk, probability, chance, coincidence—they
From playlist Prob and Stats

Zorn's Lemma, The Well-Ordering Theorem, and Undefinability (Version 2.0)
Zorn's Lemma and The Well-ordering Theorem are seemingly straightforward statements, but they give incredibly mind-bending results. Orderings, Hasse Diagrams, and the Ordinals / set theory will come up in this video as tools to get a better view of where the "proof" of Zorn's lemma comes f
From playlist The New CHALKboard

Wolfram Physics Project: Working Session Thursday, July 23, 2020 [Metamathematics | Part 1]
This is a Wolfram Physics Project progress update at the Wolfram Summer School. Originally livestreamed at: https://twitch.tv/stephen_wolfram Stay up-to-date on this project by visiting our website: http://wolfr.am/physics Check out the announcement post: http://wolfr.am/physics-announce
From playlist Wolfram Physics Project Livestream Archive

Wolfram Physics Project: a Conversation on Current Work (Jan. 26, 2021)
This is a Wolfram Physics Project conversation on our continuing efforts to make progress on the fundamental theory of physics. Begins at 3:00 Originally livestreamed at: https://twitch.tv/stephen_wolfram Stay up-to-date on this project by visiting our website: http://wolfr.am/physics Ch
From playlist Wolfram Physics Project Livestream Archive

Geometric Algebra in 2D: complex numbers without the square root of minus one - Russell Goyder
Russell Goyder introduces geometric algebra from scratch, explaining how you can *multiply* vectors in a sensible way, that is deeply related to the geometry of rotations and reflections in space. After walking us through the basics, he shows how rotors represent rotations in the setting o
From playlist metauni festival 2023

This is part of a series of lectures on the Zermelo-Fraenkel axioms for set theory. We discuss the powerset axiom, the strongest of the ZF axioms, and explain why the notion of a powerset is so hard to pin down precisely. For the other lectures in the course see https://www.youtube.com
From playlist Zermelo Fraenkel axioms
