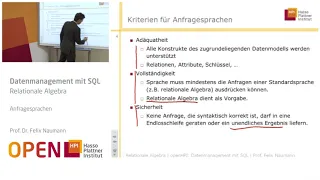
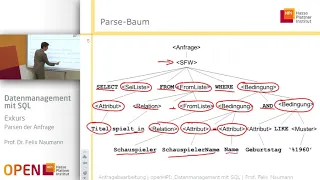
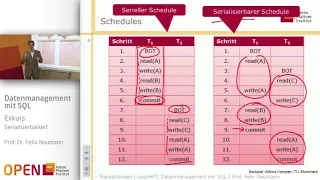
The sequence that grows remarkably large, then drops to zero!
Goodstein sequences can get larger than Graham's number and the growth rate can be faster than Ackermann’s function. In fact, these sequences grow at such an incredible rate, that the theorem literally cannot be proven using first order arithmetic and can only be proven using a stronger sy
From playlist Summer of Math Exposition 2 videos

Der Nürnberger Prozess - Die Verteidigung (4/8) / Hauptkriegsverbrecher-Prozess
Annektion von Österreich, Ernst Kaltenbrunnder, NSDAP, Chef des Reichssicherheitshauptamtes, Machtzentrale der SS, Mauthausen, Kommandant von Ausschwitz, Konzentrationslager, Berlin, Oranienburg, namenlose Häftlinge, Rüstungsindustrie, ungarische Juden, Ankläger, Alfred Rosenberg, Lehre de
From playlist Der Nürnberger Prozess - Die Verteidigung

This is part of a series of lectures on the Zermelo-Fraenkel axioms for set theory. We discuss the axiom of infinity, and give some examples of models where it does not hold. For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj52EKVgPi-p50fRP2_SbG
From playlist Zermelo Fraenkel axioms

Ultraproducts: What are they good for?
From playlist Workshop on Model Theory, Differential/Difference Algebra, and Applications

Title: Constructive Bounds from Ultraproducts and Noetherianity
From playlist Spring 2016

Strong and Weak Epsilon Nets and Their Applications - Noga Alon
Noga Alon Tel Aviv University; Institute for Advanced Study November 7, 2011 I will describe the notions of strong and weak epsilon nets in range spaces, and explain briefly some of their many applications in Discrete Geometry and Combinatorics, focusing on several recent results in the in
From playlist Mathematics

Programming Loops vs Recursion - Computerphile
Programming loops are great, but there's a point where they aren't enough. Professor Brailsford explains. EXTRA BITS: https://youtu.be/DVG5G1V8Zx0 The Most Difficult Program to Compute?: https://youtu.be/i7sm9dzFtEI What on Earth is Recursion?: https://youtu.be/Mv9NEXX1VHc Reverse Poli
From playlist Subtitled Films

Title: Differential Kernels and Bounds for the Consistency of Differential Equations
From playlist Differential Algebra and Related Topics VII (2016)

The Enormous TREE(3) - Numberphile
Professor Tony Padilla on the epic number, TREE(3). Continues at: https://youtu.be/IihcNa9YAPk More links & stuff in full description below ↓↓↓ Graham's Number: http://bit.ly/G_Number Numberphile is supported by the Mathematical Sciences Research Institute (MSRI): http://bit.ly/MSRINumbe
From playlist Tony Padilla on Numberphile

26C3: Chaos-Familien-Duell 6/12
Clip 6/12 Speakers: Alexander Brock, Marcel Ackermann Zwei Chaos-Familien treten gegeneinander an, doch es kann nur eine geben. Team-Anmeldungen sind begrenzt! Meldet Euch im Event-Wiki an: http://events.ccc.de/congress/2009/wiki/Chaos-Familien-Duell For more information go to: h
From playlist 26C3: Here be dragons day 1

Gram-Schmidt (Gram-Schmidt'sches Orthonormalisierungsverfahren)
Abonniert den Kanal oder unterstützt ihn auf Steady: https://steadyhq.com/en/brightsideofmaths Ihr werdet direkt informiert, wenn ich einen Livestream anbiete. Das Gram-Schmidtsche Orthonormalisierungsverfahren ist einer der wichtigsten Verfahren bzw. Algorithmen in den Grundlagen der li
From playlist Lineare Algebra

The Most Difficult Program to Compute? - Computerphile
The story of recursion continues as Professor Brailsford explains one of the most difficult programs to compute: Ackermann's function. Professor Brailsford's programs: http://bit.ly/1nhKtW4 Follow Up Film from the Prof in response to this film: https://www.youtube.com/watch?v=uNACwX-O5l
From playlist Subtitled Films