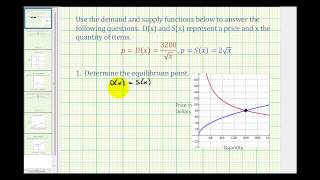
General topology | Limit sets | Topology
Accumulation point
In mathematics, a limit point, accumulation point, or cluster point of a set in a topological space is a point that can be "approximated" by points of in the sense that every neighbourhood of with respect to the topology on also contains a point of other than itself. A limit point of a set does not itself have to be an element of There is also a closely related concept for sequences. A cluster point or accumulation point of a sequence in a topological space is a point such that, for every neighbourhood of there are infinitely many natural numbers such that This definition of a cluster or accumulation point of a sequence generalizes to nets and filters. The similarly named notion of a limit point of a sequence (respectively, a limit point of a filter, a limit point of a net) by definition refers to a point that the sequence converges to (respectively, the filter converges to, the net converges to). Importantly, although "limit point of a set" is synonymous with "cluster/accumulation point of a set", this is not true for sequences (nor nets or filters). That is, the term "limit point of a sequence" is not synonymous with "cluster/accumulation point of a sequence". The limit points of a set should not be confused with adherent points (also called points of closure) for which every neighbourhood of contains a point of (that is, any point belonging to closure of the set). Unlike for limit points, an adherent point of may be itself. A limit point can be characterized as an adherent point that is not an isolated point. Limit points of a set should also not be confused with boundary points. For example, is a boundary point (but not a limit point) of the set in with standard topology. However, is a limit point (though not a boundary point) of interval in with standard topology (for a less trivial example of a limit point, see the first caption). This concept profitably generalizes the notion of a limit and is the underpinning of concepts such as closed set and topological closure. Indeed, a set is closed if and only if it contains all of its limit points, and the topological closure operation can be thought of as an operation that enriches a set by uniting it with its limit points. (Wikipedia).