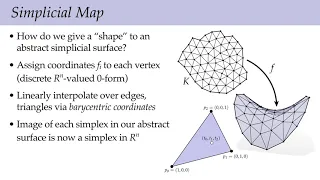
Abstract cell complex
In mathematics, an abstract cell complex is an abstract set with Alexandrov topology in which a non-negative integer number called dimension is assigned to each point. The complex is called “abstract” since its points, which are called “cells”, are not subsets of a Hausdorff space as is the case in Euclidean and CW complexes. Abstract cell complexes play an important role in image analysis and computer graphics. (Wikipedia).