What is a Vector Space? (Abstract Algebra)
Vector spaces are one of the fundamental objects you study in abstract algebra. They are a significant generalization of the 2- and 3-dimensional vectors you study in science. In this lesson we talk about the definition of a vector space and give a few surprising examples. Be sure to su
From playlist Abstract Algebra
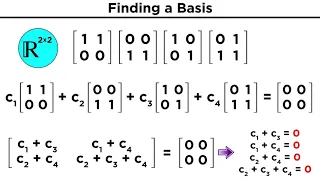
Now we know about vector spaces, so it's time to learn how to form something called a basis for that vector space. This is a set of linearly independent vectors that can be used as building blocks to make any other vector in the space. Let's take a closer look at this, as well as the dimen
From playlist Mathematics (All Of It)

When learning linear algebra, we will frequently hear the term "vector space". What is that? What are the requirements for being considered a vector space? Let's go over the properties of closure that are associated with vector spaces so that we can understand this important concept. Scri
From playlist Mathematics (All Of It)

A WEIRD VECTOR SPACE: Building a Vector Space with Symmetry | Nathan Dalaklis
We'll spend time in this video on a weird vector space that can be built by developing the ideas around symmetry. In the process of building a vector space with symmetry at its core, we'll go through a ton of different ideas across a handful of mathematical fields. Naturally, we will start
From playlist The New CHALKboard

This video explains the definition of a vector space and provides examples of vector spaces.
From playlist Vector Spaces

Orbit of a set in abstract algebra
In this video we start to take a look at the orbit-stabilizer theorem. Our first stop is the orbit of a set. The orbit is created by taking an arbitrary element of a set and acting on that element by all the elements in the set of an an arbitrary group. In this video, we look at a few p
From playlist Abstract algebra

What exactly is space? Brian Greene explains what the "stuff" around us is. Subscribe to our YouTube Channel for all the latest from World Science U. Visit our Website: http://www.worldscienceu.com/ Like us on Facebook: https://www.facebook.com/worldscienceu Follow us on Twitter: https:
From playlist Science Unplugged: Physics

What is a Vector Space? Definition of a Vector space.
From playlist Linear Algebra

Now that we know what vector spaces are, let's learn about subspaces. These are smaller spaces contained within a larger vector space that are themselves vector spaces. Script by Howard Whittle Watch the whole Mathematics playlist: http://bit.ly/ProfDaveMath Classical Physics Tutorials:
From playlist Mathematics (All Of It)

Stefaan Vaes: Cohomology and L2-Betti numbers for subfactors and quasi-regular inclusions
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Analysis and its Applications

Twisted generating functions and the nearby Lagrangian conjecture - Sylvain Courte
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Topic: Twisted generating functions and the nearby Lagrangian conjecture Speaker: Sylvain Courte Affiliation: Université Grenoble Alpes Date: February 26, 2021 For more video please visit http://video.ias.edu Courte-2021-02
From playlist Mathematics
What is a Tensor? Lesson 18: The covariant derivative continued
What is a Tensor? Lesson 18: The covariant derivative continued This lesson covers some of the "coordinate free" language used to describe the covariant derivative. As a whole this lecture is optional. However, becoming comfortable with coordinate free language is probably a good idea. I
From playlist What is a Tensor?

Math 060 101817C Matrix Transformations of Linear Transformations
Recall: If linear transformations agree on a basis, then they are equal. Recall: To each matrix A corresponds a linear transformation (left-multiplication by A). Theorem: Every linear transformation between Euclidean spaces corresponds to left-multiplication by some matrix. Example. Ex
From playlist Course 4: Linear Algebra (Fall 2017)

Jérémy Faupin : Scattering theory for Lindblad operators
Abstract: In this talk, I will consider a quantum particle interacting with a target. The target is supposed to be localized and the dynamics of the particle is supposed to be generated by a Lindbladian acting on the space of trace class operators. I will discuss scattering theory for such
From playlist Mathematical Physics

Alex Amenta: Gamma-radonifying operators in harmonic and stochastic analysis
The lecture was held within the of the Hausdorff Junior Trimester Program: Randomness, PDEs and Nonlinear Fluctuations. Abstract: Various theorems in harmonic and stochastic analysis (e.g. Littlewood-Paley theorems, the Itô isometry) represent the norm of a function in terms of a square f
From playlist HIM Lectures: Junior Trimester Program "Randomness, PDEs and Nonlinear Fluctuations"

Sept. 17, Chapter 4 (Linear algebra)
From playlist Fall 2020 Course
Lecture 3 | Modern Physics: Quantum Mechanics (Stanford)
Lecture 3 of Leonard Susskind's Modern Physics course concentrating on Quantum Mechanics. Recorded January 28, 2008 at Stanford University. This Stanford Continuing Studies course is the second of a six-quarter sequence of classes exploring the essential theoretical foundations of mode
From playlist Course | Modern Physics: Quantum Mechanics

Robert Eymard: Gradient Discretisations: Tools and Applications
Some convergence properties for the approximation of second order elliptic problems with a variety of boundary conditions (homogeneous Dirichlet, homogeneous or non-homogeneous Neumann or Fourier boundary conditions), using a given discretisation method, can be obtained when this method is
From playlist Numerical Analysis and Scientific Computing

Equivalence Relations Definition and Examples
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Equivalence Relations Definition and Examples. This video starts by defining a relation, reflexive relation, symmetric relation, transitive relation, and then an equivalence relation. Several examples are given.
From playlist Abstract Algebra

33 Sritharan - Stochastic Navier-Stokes equations - solvability & control
PROGRAM NAME :WINTER SCHOOL ON STOCHASTIC ANALYSIS AND CONTROL OF FLUID FLOW DATES Monday 03 Dec, 2012 - Thursday 20 Dec, 2012 VENUE School of Mathematics, Indian Institute of Science Education and Research, Thiruvananthapuram Stochastic analysis and control of fluid flow problems have
From playlist Winter School on Stochastic Analysis and Control of Fluid Flow