
Visual Group Theory, Lecture 1.4: Group presentations
Visual Group Theory, Lecture 1.4: Group presentations We begin this lecture by learning how to take a Cayley diagram and label its nodes with the elements of a group. Such a labeled diagram can function as a "group calculator". It leads to the notion of a "group presentation", which is a
From playlist Visual Group Theory

Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra

Visual Group Theory, Lecture 1.6: The formal definition of a group
Visual Group Theory, Lecture 1.6: The formal definition of a group At last, after five lectures of building up our intuition of groups and numerous examples, we are ready to present the formal definition of a group. We conclude by proving several basic properties that are not built into t
From playlist Visual Group Theory
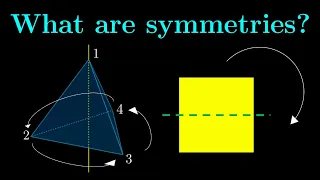
Chapter 1: Symmetries, Groups and Actions | Essence of Group Theory
Start of a video series on intuitions of group theory. Groups are often introduced as a kind of abstract algebraic object right from the start, which is not good for developing intuitions for first-time learners. This video series hopes to help you develop intuitions, which are useful in u
From playlist Essence of Group Theory

What is a Group? | Abstract Algebra
Welcome to group theory! In today's lesson we'll be going over the definition of a group. We'll see the four group axioms in action with some examples, and some non-examples as well which violate the axioms and are thus not groups. In a fundamental way, groups are structures built from s
From playlist Abstract Algebra

Group Definition (expanded) - Abstract Algebra
The group is the most fundamental object you will study in abstract algebra. Groups generalize a wide variety of mathematical sets: the integers, symmetries of shapes, modular arithmetic, NxM matrices, and much more. After learning about groups in detail, you will then be ready to contin
From playlist Abstract Algebra

A group is (in a sense) the simplest structure in which we can do the familiar tasks associated with "algebra." First, in this video, we review the definition of a group.
From playlist Modern Algebra - Chapter 15 (groups)

This is lecture 1 of an online mathematics course on group theory. This lecture defines groups and gives a few examples of them.
From playlist Group theory

Group Theory for Physicists (Definitions with Examples)
In this video, we cover the most basic points that a physicist should know about group theory. Along the way, we'll give you lots of examples that illustrate each step. 00:00 Introduction 00:11 Definition of a Group 00:59 (1) Closure 01:34 (2) Associativity 02:02 (3) Identity Element 03:
From playlist Mathematical Physics

CTNT 2020 - G-Valued Crystalline Deformation Rings in the Fontaine-Laffaille Range - Jeremy Booher
The Connecticut Summer School in Number Theory (CTNT) is a summer school in number theory for advanced undergraduate and beginning graduate students, to be followed by a research conference. For more information and resources please visit: https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2020 - Conference Videos

Donald Cartwright : Construction of lattices defining fake projective planes - lecture 4
Recording during the meeting "Ball Quotient Surfaces and Lattices " the February 26, 2019 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Ma
From playlist Algebraic and Complex Geometry

Supercuspidal representations of GL(n)... by a Galois involution (Lecture 2) by Vincent Sécherre
PROGRAM : ALGEBRAIC AND ANALYTIC ASPECTS OF AUTOMORPHIC FORMS ORGANIZERS : Anilatmaja Aryasomayajula, Venketasubramanian C G, Jurg Kramer, Dipendra Prasad, Anandavardhanan U. K. and Anna von Pippich DATE & TIME : 25 February 2019 to 07 March 2019 VENUE : Madhava Lecture Hall, ICTS Banga
From playlist Algebraic and Analytic Aspects of Automorphic Forms 2019

Calculations with Matrix groups over the integers by Alexander Hulpke
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

VassarStats - Clinical Block 2 Example
Lecturer: Dr. Erin M. Buchanan Missouri State University Spring 2017 This video covers how to calculate rates, relative risk, odds, odds ratios, relative risk reduction, and numbers needed to treat. Lecture materials and assignments available at statisticsofdoom.com. https://statistics
From playlist Advanced Statistics Videos

Representation growth, rational singularities, symplectic volume, and random matrices by Nir Avni
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation

Representations of pp-adic groups - Jessica Fintzen
Short talks by postdoctoral members Topic: Representations of pp-adic groups Speaker: Jessica Fintzen Affiliation: Member, School of Mathematics Date: September 27, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Imprimitive irreducible representations of finite quasisimple groups by Gerhard Hiss
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

Modulo p Representations of GL_2 (K) (Lecture 2) by Benjamin Schraen
Program Recent developments around p-adic modular forms (ONLINE) ORGANIZERS: Debargha Banerjee (IISER Pune, India) and Denis Benois (University of Bordeaux, France) DATE: 30 November 2020 to 04 December 2020 VENUE: Online This is a follow up of the conference organized last year arou
From playlist Recent Developments Around P-adic Modular Forms (Online)

Endomorphisms of certain superelliptic jacobians and l-adic (..) - Zarhin - Workshop 2 - CEB T2 2019
Yuri Zarhin (Pennsylvania State University) / 28.06.2019 Endomorphisms of certain superelliptic jacobians and l-adic Lie algebras The subject of this talk is a certain explicitly constructed class of superelliptic jacobians defined over global fields with small endomorphism rings. We al
From playlist 2019 - T2 - Reinventing rational points

Visual Group Theory, Lecture 3.4: Direct products
Visual Group Theory, Lecture 3.4: Direct products There is a natural way to put a group structure on the Cartesian product of two groups. In this lecture, we introduce this concept algebraically, and show several different ways to visualize this, using tools such as Cayley diagrams and mu
From playlist Visual Group Theory