
Zero dimensional valuations on equicharacteristic (...) - B. Teissier - Workshop 2 - CEB T1 2018
Bernard Teissier (IMJ-PRG) / 06.03.2018 Zero dimensional valuations on equicharacteristic noetherian local domains. A study of those valuations based, in the case where the domain is complete, on the relations between the elements of a minimal system of generators of the value semigroup o
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

Understanding Wealth Inequality
We've talked about public goods and externalities, and one negative externality associated with economic decisions is wealth inequality. A certain measure of wealth inequality is expected and desirable for any economy. But when this becomes extreme, as it is in the United States and many o
From playlist Economics

Yves André - Direct summand conjecture and perfectoid Abhyankar lemma: an overview
Séminaire Paris Pékin Tokyo / Mercredi 2 novembre 2016 According to Hochster's direct summand conjecture (1973), a regular ring R is a direct summand, as an R-module, of every finite extension ring. We shall outline our recent proof which relies on perfectoid techniques. Similar arguments
From playlist Conférences Paris Pékin Tokyo

Frédéric Mangolte: Algebraic models of the line in the real affine plane
Abstract: We study the following real version of the famous Abhyankar-Moh Theorem: Which real rational map from the affine line to the affine plane, whose real part is a non-singular real closed embedding of ℝ into ℝ^2, is equivalent, up to a birational diffeomorphism of the plane, to the
From playlist Algebraic and Complex Geometry
In this video, I state and prove Chebyshev's inequality, and its cousin Markov's inequality. Those inequalities tell us how big an integrable function can really be. Enjoy!
From playlist Real Analysis

Solving an absolute value inequality using an and compound inequality
👉 Learn how to solve absolute value inequalities. The absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value inequality, we create the two cases of absolute value problems
From playlist Solve Absolute Value Inequalities

Solving and graphing an inequality
👉 Learn how to solve multi-step linear inequalities having parenthesis. An inequality is a statement in which one value is not equal to the other value. An inequality is linear when the highest exponent in its variable(s) is 1. (i.e. there is no exponent in its variable(s)). A multi-step l
From playlist Solve and Graph Inequalities | Multi-Step With Parenthesis

Learn how to solve a multi step inequality and graph the solution
👉 Learn how to solve multi-step linear inequalities having parenthesis. An inequality is a statement in which one value is not equal to the other value. An inequality is linear when the highest exponent in its variable(s) is 1. (i.e. there is no exponent in its variable(s)). A multi-step l
From playlist Solve and Graph Inequalities | Multi-Step With Parenthesis

Solving an absolute value inequality
👉 Learn how to solve absolute value inequalities. The absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value inequality, we create the two cases of absolute value problems
From playlist Solve Absolute Value Inequalities

How to solve a one variable absolute value inequality or statement
👉 Learn how to solve absolute value inequalities. The absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value inequality, we create the two cases of absolute value problems
From playlist Solve Absolute Value Inequalities
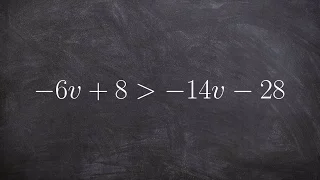
Solving and graphing a linear inequality
👉 Learn how to solve multi-step linear inequalities having no parenthesis. An inequality is a statement in which one value is not equal to the other value. An inequality is linear when the highest exponent in its variable(s) is 1. (i.e. there is no exponent in its variable(s)). A multi-ste
From playlist Solve and Graph Inequalities | Multi-Step Without Parenthesis

Solving and graphing an absolute value inequality with an or inequality
👉 Learn how to solve absolute value inequalities. The absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value inequality, we create the two cases of absolute value problems
From playlist Solve Absolute Value Inequalities

How to Solve Inequalities (NancyPi)
MIT grad explains solving inequalities. This video focuses on solving linear inequalities. It shows when to switch the sign of the inequality, if you divide or multiply by a negative number, and is an introduction to how to solve inequalities in algebra. To skip ahead: 1) For a basic examp
From playlist Algebra

Compound Inequalities 9 Examples including Fractions & Interval Notation
I start by defining Compound Inequalities & explaining the difference between "and" and "or" statements Inequality to Number Line examples at 2:03 7:01 8:44 Number Line to Inequality examples at 11:01 14:19 16:55 These examples include Interval Notation. Solving a Compound Inequality exa
From playlist Algebra 1

Concentration of quantum states from quantum functional (...) - N. Datta - Workshop 2 - CEB T3 2017
Nilanjana Datta / 24.10.17 Concentration of quantum states from quantum functional and transportation cost inequalities Quantum functional inequalities (e.g. the logarithmic Sobolev- and Poincaré inequalities) have found widespread application in the study of the behavior of primitive q
From playlist 2017 - T3 - Analysis in Quantum Information Theory - CEB Trimester

Radek Adamczak: Functional inequalities and concentration of measure II
Concentration inequalities are one of the basic tools of probability and asymptotic geo- metric analysis, underlying the proofs of limit theorems and existential results in high dimensions. Original arguments leading to concentration estimates were based on isoperimetric inequalities, whic
From playlist Winter School on the Interplay between High-Dimensional Geometry and Probability

8ECM Invited Lecture: Rupert Frank
From playlist 8ECM Invited Lectures

Joe Neeman: Gaussian isoperimetry and related topics II
The Gaussian isoperimetric inequality gives a sharp lower bound on the Gaussian surface area of any set in terms of its Gaussian measure. Its dimension-independent nature makes it a powerful tool for proving concentration inequalities in high dimensions. We will explore several consequence
From playlist Winter School on the Interplay between High-Dimensional Geometry and Probability

Grade 7: Module 3 Lesson 12 on Inequalities
From playlist Eureka Math Grade 7 Module 3

Solving and graphing a two step absolute value inequality
👉 Learn how to solve absolute value inequalities. The absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value inequality, we create the two cases of absolute value problems
From playlist Solve Absolute Value Inequalities