
Learn to find the or probability from a tree diagram
👉 Learn how to find the conditional probability of an event. Probability is the chance of an event occurring or not occurring. The probability of an event is given by the number of outcomes divided by the total possible outcomes. Conditional probability is the chance of an event occurring
From playlist Probability

Expected Value of a Discrete Probability Distribution
This video explains how to determine the expected value or mean value of a discrete probability distribution. http://mathispower4u.com
From playlist Probability

Ex: Determine Conditional Probability from a Table
This video provides two examples of how to determine conditional probability using information given in a table.
From playlist Probability

Ex: Determine Probability Given Odds
This video explains how to determine probability given odds.
From playlist Probability
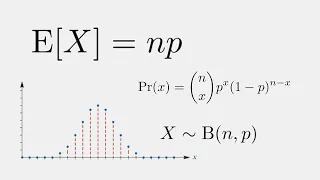
Expected Value of a Binomial Probability Distribution
Today, we derive the formula to find the expected value or the mean of a discrete random variable which follows the binomial probability distribution.
From playlist Probability

How to find the probability of consecutive events
👉 Learn how to find the conditional probability of an event. Probability is the chance of an event occurring or not occurring. The probability of an event is given by the number of outcomes divided by the total possible outcomes. Conditional probability is the chance of an event occurring
From playlist Probability

(New Version Available) Conditional Probability
New Version: Fixes an error at 7:00: https://youtu.be/WgsxhWPAo4c This video explains how to determine conditional probability. http://mathispower4u.yolasite.com/
From playlist Counting and Probability

Determining the conditional probability from a contingency table
👉 Learn how to find the conditional probability of an event. Probability is the chance of an event occurring or not occurring. The probability of an event is given by the number of outcomes divided by the total possible outcomes. Conditional probability is the chance of an event occurring
From playlist Probability

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Introduction to Probability
From playlist Statistics
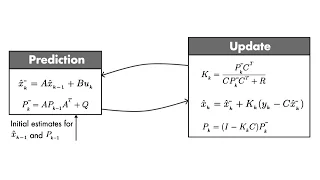
Optimal State Estimator Algorithm | Understanding Kalman Filters, Part 4
Download our Kalman Filter Virtual Lab to practice linear and extended Kalman filter design of a pendulum system with interactive exercises and animations in MATLAB and Simulink: https://bit.ly/3g5AwyS Discover the set of equations you need to implement a Kalman filter algorithm. You’ll l
From playlist Understanding Kalman Filters

Lecture 1 | Modern Physics: Statistical Mechanics
March 30, 2009 - Leonard Susskind discusses the study of statistical analysis as calculating the probability of things subject to the constraints of a conserved quantity. Susskind introduces energy, entropy, temperature, and phase states as they relate directly to statistical mechanics.
From playlist Lecture Collection | Modern Physics: Statistical Mechanics

Oxford 4b The Argument Concerning Induction
A course by Peter Millican from Oxford University. Course Description: Dr Peter Millican gives a series of lectures looking at Scottish 18th Century Philosopher David Hume and the first book of his Treatise of Human Nature. Taken from: https://podcasts.ox.ac.uk/series/introduction-david
From playlist Oxford: Introduction to David Hume's Treatise of Human Nature Book One | CosmoLearning Philosophy

Probabilistic inverse problems (Lecture 1) by Daniela Calvetti
DISCUSSION MEETING WORKSHOP ON INVERSE PROBLEMS AND RELATED TOPICS (ONLINE) ORGANIZERS: Rakesh (University of Delaware, USA) and Venkateswaran P Krishnan (TIFR-CAM, India) DATE: 25 October 2021 to 29 October 2021 VENUE: Online This week-long program will consist of several lectures by
From playlist Workshop on Inverse Problems and Related Topics (Online)

21. Hypothesis Testing and Random Walks
MIT 6.262 Discrete Stochastic Processes, Spring 2011 View the complete course: http://ocw.mit.edu/6-262S11 Instructor: Robert Gallager License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.262 Discrete Stochastic Processes, Spring 2011

Christian Jutten - Petite visite guidée de la séparation de sources
GIPSA-Lab, Prix Science et Innovation 2016 Réalisation technique : Antoine Orlandi (GRICAD) | Tous droits réservés
From playlist Des mathématiciens primés par l'Académie des Sciences 2017

Mikhail Lyubich: Story of the Feigenbaum point
HYBRID EVENT Recorded during the meeting "Advancing Bridges in Complex Dynamics" the September 23, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Luca Récanzone Find this video and other talks given by worldwide mathematicians on CIRM's Audi
From playlist Dynamical Systems and Ordinary Differential Equations

5 Idealisms & their Refutations - Kant's Critique of Pure Reason (Dan Robinson)
Dan Robinson gives the 5th lecture in a series of 8 on Immanuel Kant's Critique of Pure Reason. All 8 lectures: https://www.youtube.com/playlist?list=PLhP9EhPApKE_OdgqNgL0AJX9-gwr4tmLw The very possibility of self-awareness (an "inner sense" with content) requires an awareness of an exte
From playlist Kant's Critique of Pure Reason - Dan Robinson

How To Tackle Our Inverse Problem by Wolfgang Waltenberger
Discussion Meeting : Hunting SUSY @ HL-LHC (ONLINE) ORGANIZERS : Satyaki Bhattacharya (SINP, India), Rohini Godbole (IISc, India), Kajari Majumdar (TIFR, India), Prolay Mal (NISER-Bhubaneswar, India), Seema Sharma (IISER-Pune, India), Ritesh K. Singh (IISER-Kolkata, India) and Sanjay Kuma
From playlist HUNTING SUSY @ HL-LHC (ONLINE) 2021

Shannon 100 - 26/10/2016 - Elisabeth GASSIAT
Entropie, compression et statistique Elisabeth Gassiat (Université de Paris-Sud) Claude Shannon est l'inventeur de la théorie de l'information. Il a introduit la notion d'entropie comme mesure de l'information contenue dans un message vu comme provenant d'une source stochastique et démon
From playlist Shannon 100

Probability - Quantum and Classical
The Law of Large Numbers and the Central Limit Theorem. Probability explained with easy to understand 3D animations. Correction: Statement at 13:00 should say "very close" to 50%.
From playlist Physics