
Learn how to evaluate a limit by factoring
👉 Learn how to evaluate the limit of a function involving rational expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct subst
From playlist Evaluate the Limit (PC)

(ML 6.1) Maximum a posteriori (MAP) estimation
Definition of maximum a posteriori (MAP) estimates, and a discussion of pros/cons. A playlist of these Machine Learning videos is available here: http://www.youtube.com/view_play_list?p=D0F06AA0D2E8FFBA
From playlist Machine Learning

Ex : Determine The Value of a Derivative using the Limit Definition (Rational)
This video explains how to determine the value of a derivative at a given value of x using the limit definition of the derivative. The results are verified graphically http://mathispower4u.com
From playlist Introduction and Formal Definition of the Derivative

Find a Function and x-value From Limit Definition of the Derivative
This video explains how to determine a function and x-value given the limit definition of the derivative.
From playlist Introduction and Formal Definition of the Derivative

Ex : Determine The Value of a Derivative using the Limit Definition (Quadratic)
This video explains how to determine the value of a derivative at a given value of x using the limit definition of the derivative. The results are verified graphically http://mathispower4u.com
From playlist Introduction and Formal Definition of the Derivative

Evaluating a limit by factoring
👉 Learn how to evaluate the limit of a function involving rational expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct subst
From playlist Evaluate the Limit (PC)
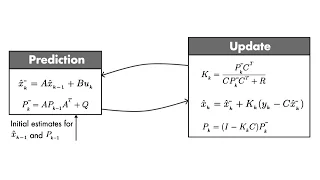
Optimal State Estimator Algorithm | Understanding Kalman Filters, Part 4
Download our Kalman Filter Virtual Lab to practice linear and extended Kalman filter design of a pendulum system with interactive exercises and animations in MATLAB and Simulink: https://bit.ly/3g5AwyS Discover the set of equations you need to implement a Kalman filter algorithm. You’ll l
From playlist Understanding Kalman Filters

Evaluate the left hand limit at an asymptote algebraically
👉 Learn how to evaluate the limit of a function involving rational expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct subst
From playlist Evaluate the Limit (PC)

Evaluate the limit at a hole by factoring
👉 Learn how to evaluate the limit of a function involving rational expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct subst
From playlist Evaluate the Limit (PC)

Christian Jutten - Petite visite guidée de la séparation de sources
GIPSA-Lab, Prix Science et Innovation 2016 Réalisation technique : Antoine Orlandi (GRICAD) | Tous droits réservés
From playlist Des mathématiciens primés par l'Académie des Sciences 2017

[BOURBAKI 2017] 17/06/2017 - 3/4 - Frédéric ROUSSET
Solutions faibles de l'équation de Navier-Stokes des fluides compressibles [d'après A. Vasseur et C. Yu] ---------------------------------- Vous pouvez nous rejoindre sur les réseaux sociaux pour suivre nos actualités. Facebook : https://www.facebook.com/InstitutHenriPoincare/ Twitter :
From playlist BOURBAKI - 2017

Martina Hofmanova: Global solutions to elliptic and parabolic Φ4 models in Euclidean space
Abstract: I will present some recent results on global solutions to singular SPDEs on ℝd with cubic nonlinearities and additive white noise perturbation, both in the elliptic setting in dimensions d=4,5 and in the parabolic setting for d=2,3. A motivation for considering these equations is
From playlist Probability and Statistics

Multicontinuum Model for the Wave Equation in a High Contrast Laminated Beam by Gregory Panasenko
DISCUSSION MEETING Multi-Scale Analysis: Thematic Lectures and Meeting (MATHLEC-2021, ONLINE) ORGANIZERS: Patrizia Donato (University of Rouen Normandie, France), Antonio Gaudiello (Università degli Studi di Napoli Federico II, Italy), Editha Jose (University of the Philippines Los Baño
From playlist Multi-scale Analysis: Thematic Lectures And Meeting (MATHLEC-2021) (ONLINE)

Muhammad Hassan - Development of a posteriori error estimates for the coupled cluster equations
Recorded 03 May 2022. Muhammad Hassan of Sorbonne Université, Laboratoire Jacques-Louis Lions, presents "Towards the development of a posteriori error estimates for the coupled cluster equations" at IPAM's Large-Scale Certified Numerical Methods in Quantum Mechanics Workshop. Abstract: Cou
From playlist 2022 Large-Scale Certified Numerical Methods in Quantum Mechanics

Probabilistic inverse problems (Lecture 1) by Daniela Calvetti
DISCUSSION MEETING WORKSHOP ON INVERSE PROBLEMS AND RELATED TOPICS (ONLINE) ORGANIZERS: Rakesh (University of Delaware, USA) and Venkateswaran P Krishnan (TIFR-CAM, India) DATE: 25 October 2021 to 29 October 2021 VENUE: Online This week-long program will consist of several lectures by
From playlist Workshop on Inverse Problems and Related Topics (Online)

Ex 2: Determine a Derivative using The Limit Definition
This video determine the derivative of a basic rational function using the limit definition. It also determines the slope of a tangent line at a given value of x. Complete Video List at http://www.mathispower4u.com
From playlist Introduction and Formal Definition of the Derivative

Philippe Moireau: Data Assimilation: a deterministic vision, theory and applications. Lecture 1
Abstract: The question of using the available measurements to retrieve mathematical models characteristics (parameters, boundary conditions, initial conditions) is a key aspect of the modeling objective in biology or medicine. In a stochastic/statistical framework this question is seen as
From playlist Control Theory and Optimization

Victor Panaretos: The extrapolation of correlation
CONFERENCE Recording during the thematic meeting : "Adaptive and High-Dimensional Spatio-Temporal Methods for Forecasting " the September 29, 2022 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks
From playlist Analysis and its Applications

Shannon 100 - 26/10/2016 - Elisabeth GASSIAT
Entropie, compression et statistique Elisabeth Gassiat (Université de Paris-Sud) Claude Shannon est l'inventeur de la théorie de l'information. Il a introduit la notion d'entropie comme mesure de l'information contenue dans un message vu comme provenant d'une source stochastique et démon
From playlist Shannon 100

Ex: Determine the Derivative of a Function Using the Limit Definition (ax^2+bx+c)
This video provides an example of how to determine the derivative of a quadratic function using the limit definition of the derivative.
From playlist Introduction and Formal Definition of the Derivative