
Abstract Algebra - 11.1 Fundamental Theorem of Finite Abelian Groups
We complete our study of Abstract Algebra in the topic of groups by studying the Fundamental Theorem of Finite Abelian Groups. This tells us that every finite abelian group is a direct product of cyclic groups of prime-power order. Video Chapters: Intro 0:00 Before the Fundamental Theorem
From playlist Abstract Algebra - Entire Course
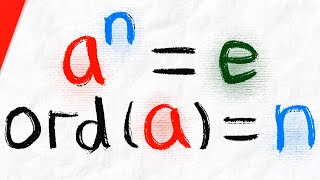
Order of Elements in a Group | Abstract Algebra
We introduce the order of group elements in this Abstract Algebra lessons. We'll see the definition of the order of an element in a group, several examples of finding the order of an element in a group, and we will introduce two basic but important results concerning distinct powers of ele
From playlist Abstract Algebra

Abstract Algebra - 3.1 Finite Groups and Subgroups: Terminology and Notation
Most of this chapter will revolve around the idea of a subgroup. However, we must begin by being able to differentiate between a finite group and infinite group. We look at some notation and definitions (order of a group, order of an element) before jumping into subgroups. Video Chapters:
From playlist Abstract Algebra - Entire Course

Simple groups, Lie groups, and the search for symmetry II | Math History | NJ Wildberger
This is the second video in this lecture on simple groups, Lie groups and manifestations of symmetry. During the 19th century, the role of groups shifted from its origin in number theory and the theory of equations to its role in describing symmetry in geometry. In this video we talk abou
From playlist MathHistory: A course in the History of Mathematics

Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra

What is a Group? | Abstract Algebra
Welcome to group theory! In today's lesson we'll be going over the definition of a group. We'll see the four group axioms in action with some examples, and some non-examples as well which violate the axioms and are thus not groups. In a fundamental way, groups are structures built from s
From playlist Abstract Algebra

Every Group is a Quotient of a Free Group
First isomorphism theorem: https://youtu.be/ssVIJO5uNeg An explanation of a proof that every finite group is a quotient of a free group. A similar proof also applies to infinite groups because we can consider a free group on an infinite number of elements! Group Theory playlist: https://
From playlist Group Theory

Representation Theory(Repn Th) 2 by Gerhard Hiss
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

David Rydh. Local structure of algebraic stacks and applications
Abstract: Some natural moduli problems, such as moduli of sheaves and moduli of singular curves, give rise to stacks with infinite stabilizers that are not known to be quotient stacks. The local structure theorem states that many stacks locally look like the quotient of a scheme by the act
From playlist CORONA GS

Representation Theory(Repn Th) 1 by Gerhard Hiss
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

C. Leininger - Teichmüller spaces and pseudo-Anosov homeomorphism (Part 2)
I will start by describing the Teichmuller space of a surface of finite type from the perspective of both hyperbolic and complex structures and the action of the mapping class group on it. Then I will describe Thurston's compactification of Teichmuller space, and state his classification t
From playlist Ecole d'été 2018 - Teichmüller dynamics, mapping class groups and applications

Dynamics on character varieties - William Goldman
Character Varieties, Dynamics and Arithmetic Topic: Dynamics on character varieties Speaker: William Goldman Affiliation: University of Maryland; Member, School of Mathematics Date: November 10, 2021 In these two talks, I will describe how the classification of locally homogeneous geomet
From playlist Mathematics

This lecture is part of an online math course on group theory. We review free abelian groups, then construct free (non-abelian) groups, and show that they are given by the set of reduced words, and as a bonus find that they are residually finite.
From playlist Group theory

Representation Theory(Repn Th) 3 by Gerhard Hiss
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

Simple Groups - Abstract Algebra
Simple groups are the building blocks of finite groups. After decades of hard work, mathematicians have finally classified all finite simple groups. Today we talk about why simple groups are so important, and then cover the four main classes of simple groups: cyclic groups of prime order
From playlist Abstract Algebra

John Pardon: Virtual fundamental cycles and contact homology
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Jean-Morlet Chair - Lalonde/Teleman

Flag manifolds over semifields II - Xuhua He
Workshop on Representation Theory and Geometry Topic: Flag manifolds over semifields II Speaker: Xuhua He Affiliation: Chinese University of Hong Kong; Member, School of Mathematics Date: April 03, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

Barak Weiss - Examples for the horocycle owon moduli spaces
PROGRAM: RECENT TRENDS IN ERGODIC THEORY AND DYNAMICAL SYSTEMS DATES: Tuesday 18 Dec, 2012 - Saturday 29 Dec, 2012 VENUE: Department of Mathematics,Faculty of Science, The Maharaja Sayajirao University of Baroda, Vadodara PROGRAM LINK: http://www.icts.res.in/program/ETDS2012 DESCR
From playlist Recent Trends in Ergodic Theory and Dynamical Systems

Moonshine - 1 By Suresh Govindarajan
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods
Logical challenges with abstract algebra II | Abstract Algebra Math Foundations 215 | NJ Wildberger
There is a very big jump in going from finite algebraic objects to "infinite algebraic objects". For example, there is a huge difference, if one is interested in very precise definitions, between the concept of a finite group and the concept of an "infinite group". We illustrate this imp
From playlist Math Foundations