
Depth complexity and communication games - Or Meir
Or Meir Institute for Advanced Study; Member, School of Mathematics September 30, 2013 For more videos, visit http://video.ias.edu
From playlist Mathematics

Algorithms Explained: Computational Complexity
An overview of computational complexity including the basics of big O notation and common time complexities with examples of each. Understanding computational complexity is vital to understanding algorithms and why certain constructions or implementations are better than others. Even if y
From playlist Algorithms Explained

Understanding quantum algorithms via query complexity – Andris Ambainis – ICM2018
Mathematical Aspects of Computer Science Invited Lecture 14.2 Understanding quantum algorithms via query complexity Andris Ambainis Abstract: Query complexity is a model of computation in which we have to compute a function f(x_1, …, x_N) of variables x_i which can be accessed via querie
From playlist Mathematical Aspects of Computer Science

Big O Notation: A Few Examples
This video is about Big O Notation: A Few Examples Time complexity is commonly estimated by counting the number of elementary operations (elementary operation = an operation that takes a fixed amount of time to preform) performed in the algorithm. Time complexity is classified by the nat
From playlist Computer Science and Software Engineering Theory with Briana

What are complex numbers? | Essence of complex analysis #2
A complete guide to the basics of complex numbers. Feel free to pause and catch a breath if you feel like it - it's meant to be a crash course! Complex numbers are useful in basically all sorts of applications, because even in the real world, making things complex sometimes, oxymoronicall
From playlist Essence of complex analysis

Mathematical modeling of evolving systems
Discover the multidisciplinary nature of the dynamical principles at the core of complexity science. COURSE NUMBER: CAS 522 COURSE TITLE: Dynamical Systems LEVEL: Graduate SCHOOL: School of Complex Adaptive Systems INSTRUCTOR: Enrico Borriello MODE: Online SEMESTER: Fall 2021 SESSION:
From playlist What is complex systems science?

B04 Example problem of simple harmonic oscillation
Solving an example problem of simple harmonic oscillation, which requires calculating the solution to a second order ordinary differential equation.
From playlist Physics ONE
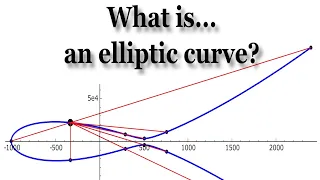
In this talk, we will define elliptic curves and, more importantly, we will try to motivate why they are central to modern number theory. Elliptic curves are ubiquitous not only in number theory, but also in algebraic geometry, complex analysis, cryptography, physics, and beyond. They were
From playlist An Introduction to the Arithmetic of Elliptic Curves

EEVblog 1470 - AC Basics Tutorial Part 3 - Complex Numbers are EASY!
Complex numbers are NOT complex! How complex numbers are used in AC circuit analysis. 00:00 - Complex Numbers 00:44 - Phasor graphical addition 01:22 - Why do calculators have the R-P and P-R buttons? 02:44 - Phasor diagram 03:59 - The AC voltage equation 04:47 - The complex plane and j v
From playlist Electronics Tutorials - AC Theory Series

EEVblog 1469 - AC Basics Tutorial - Part 2 - Phasors
Part 2 of the AC Basics tutorial series. What are phasors and doing phasor addition. In-phase, out of phase, and leading and lagging waveforms. Phi vs Theta phase angle. Leading into complex numbers in Part 3. 00:00 - AC Basics Theory 00:40 - How an AC waveform is produced 01:37 - Degrees
From playlist Electronics Tutorials - AC Theory Series

Lower bounds for subgraph isomorphism – Benjamin Rossman – ICM2018
Mathematical Aspects of Computer Science Invited Lecture 14.3 Lower bounds for subgraph isomorphism Benjamin Rossman Abstract: We consider the problem of determining whether an Erdős–Rényi random graph contains a subgraph isomorphic to a fixed pattern, such as a clique or cycle of consta
From playlist Mathematical Aspects of Computer Science

An average-case depth hierarchy theorem for Boolean - Li-Yang Tan
Computer Science/Discrete Mathematics Seminar I Topic: An average-case depth hierarchy theorem for Boolean circuits I Speaker: Li-Yang Tan Affiliation: Toyota Technological Institute, Chicago Date: Monday, April 4 We prove an average-case depth hierarchy theorem for Boolean circuits
From playlist Mathematics
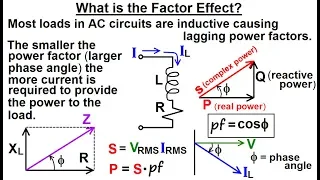
Electrical Engineering: Ch 12 AC Power (47 of 58) What is the Power Factor Effect?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain the effect of the power-factor of an AC circuit. It turns out that most loads in an AC circuit is inductive in nature. Which means there's a phase angle between the current and voltage. Typica
From playlist ELECTRICAL ENGINEERING 12 AC POWER

Solving Olympiad Level Geometry Problems with Complex Numbers #SoME2
Errata: At 9:20 the second -lambda should be replaced with +lambda At 13:09 we meant to say: "The astute scholars amongst you may have noticed that we just looked at Cartesian geometry up to this point." At 24:53 we meant to say: "We just know that D is somewhere on the line segment AC."
From playlist Summer of Math Exposition 2 videos

Calculus 2: Complex Numbers & Functions (4 of 28) Multiplying and Dividing Complex Numbers
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain how to multiply and divide complex numbers. Next video in the series can be seen at: https://youtu.be/2vAGt845gFY
From playlist CALCULUS 2 CH 11 COMPLEX NUMBERS

Visualizing Complex Number Multiplication
In this video, I discuss the rotational and scaling aspects of complex number multiplication and how both miraculously follow from the simple assumption that some object, called "i", squares to -1. I also present some animations showing the effect of complex number multiplication on a coll
From playlist Complex Numbers

What’s AC and DC (ElectroBOOM101-003)
Alternating Current and Direct Current are NOT as simple as you think, or at least that’s what some people say… But let me make it simple for you. Covered in this Episode: 00:00 Definition of AC and DC 1:13 Sinusoidal and other Waveforms 2:31 Period and Frequency (Hertz) 2:58 Angular Frequ
From playlist ElectroBOOM101

The chaotic complexity of natural numbers | Data structures in Mathematics Math Foundations 175
This is a sobering and perhaps disorienting introduction to the fact that arithmetic with bigger numbers starts to look quite different from the familiar arithmetic that we do with the small numbers we are used to. The notion of complexity is key in our treatment of this. We talk about bot
From playlist Math Foundations

