
Equivalence Relations Definition and Examples
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Equivalence Relations Definition and Examples. This video starts by defining a relation, reflexive relation, symmetric relation, transitive relation, and then an equivalence relation. Several examples are given.
From playlist Abstract Algebra

Two Equivalence Classes [a] and [b] Are Equal If and Only If a is Related to b
In this video I prove a statement surrounding relations. We have an equivalence relation on a set A and we have to show that the equivalence class of a is equal to the equivalence class of b if and only if a is related to b. If you enjoyed this video please consider liking, sharing, and
From playlist Relations

This video is a full introduction to equivalence relations. Timestamps: 0:00 What is a relation? 3:02 Terminology - A Relation defined on a Set 4:02 Equivalence Relation Definition 7:18 Reflexive 9:18 Symmetric 11:48 Transitive Thanks for watching! Comment below with questions, and make
From playlist Proofs

The picture in the lecture was taken from Wikipedia: https://en.wikipedia.org/wiki/Demographics_of_the_United_States#/media/File:USA2020dec1.png
From playlist Abstract Algebra 1
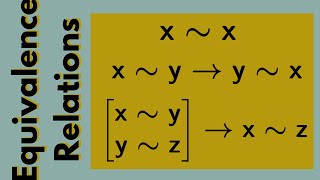
Abstract Algebra | Equivalence Relations
We give the definition of an equivalence relation and some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Put all three properties of binary relations together and you have an equivalence relation.
From playlist Abstract algebra

Important Math Proof: The Set of Equivalence Classes Partition a Set
In this video I prove a very important result in mathematics. Given an equivalence relation R on a nonempty set A, the set S of equivalence classes of A is a partition of A. Stated another way, this result says we can write A as a disjoint union of equivalence classes. The pencils I used
From playlist Relations

Cosets and equivalence class proof
Now that we have shown that the relation on G is an equivalence relation ( https://www.youtube.com/watch?v=F7OgJi6o9po ), we can go on to prove that the equivalence class containing an element is the same as the corresponding set on H (a subset of G).
From playlist Abstract algebra

Equivalence Relation on a Group Two Proofs
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Equivalence Relation on a Group Two Proofs. Given a group G and a subgroup H of G, we prove that the relation x=y if xy^{-1} is in H is an equivalence relation on G. Then cosets are defined and we prove that s_1 = s_2 iff [s_1] = [s
From playlist Abstract Algebra

Equivalence Relations -- Proof Writing 17
⭐Support the channel⭐ Patreon: https://www.patreon.com/michaelpennmath Merch: https://teespring.com/stores/michael-penn-math My amazon shop: https://www.amazon.com/shop/michaelpenn 🟢 Discord: https://discord.gg/Ta6PTGtKBm ⭐my other channels⭐ Main Channel: https://www.youtube.
From playlist Proof Writing

Some important facts about ≡ (mod n)
We prove some important facts about a very important equivalence relation on the integers -- congruence modulo n. Suggest a problem: https://forms.gle/ea7Pw7HcKePGB4my5 Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Merch: https://teespring.com/stores/micha
From playlist Proof Writing

Set Theory (Part 6): Equivalence Relations and Classes
Please feel free to leave comments/questions on the video and practice problems below! In this video, I set up equivalence relations and the canonical mapping. The idea of equivalence relation will return when we construct higher-level number systems, e.g.integers, from the natural number
From playlist Set Theory by Mathoma

Equivalence Relations and Partitions
We look at the connection between equivalence relations on a set and partitions of a set. Suggest a problem: https://forms.gle/ea7Pw7HcKePGB4my5 Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Merch: https://teespring.com/stores/michael-penn-math Personal W
From playlist Proof Writing

What is a Manifold? Lesson 14: Quotient Spaces
I AM GOING TO REDO THIS VIDEO. I have made some annotations here and annotations are not visible on mobile devices. STAY TUNED. This is a long lesson about an important topological concept: quotient spaces.
From playlist What is a Manifold?

ITHT: Part 11- Quillen Adjunctions
Credits: nLab: https://ncatlab.org/nlab/show/Introduction+to+Homotopy+Theory#QuillenAdjunctions Animation library: https://github.com/3b1b/manim My own code/modified library: https://github.com/treemcgee42/youtub... Music: ► Artist Attribution • Music By: "KaizanBlu" • Track Na
From playlist Introduction to Homotopy Theory

Measure Equivalence, Negative Curvature, Rigidity (Lecture 1) by Camille Horbez
PROGRAM: PROBABILISTIC METHODS IN NEGATIVE CURVATURE ORGANIZERS: Riddhipratim Basu (ICTS - TIFR, India), Anish Ghosh (TIFR, Mumbai, India), Subhajit Goswami (TIFR, Mumbai, India) and Mahan M J (TIFR, Mumbai, India) DATE & TIME: 27 February 2023 to 10 March 2023 VENUE: Madhava Lecture Hall
From playlist PROBABILISTIC METHODS IN NEGATIVE CURVATURE - 2023
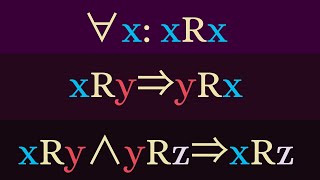
We look at the notion of an equivalence relation on a set, define an equivalence class, and consider several examples. Suggest a problem: https://forms.gle/ea7Pw7HcKePGB4my5 Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Merch: https://teespring.com/stores/
From playlist Proof Writing

Equivalences and Partitions, Axiomatic Set Theory 2 2
Defining equivalences and partitions of sets, and proving some theorems about their relations to each other. My Twitter: https://twitter.com/KristapsBalodi3 Equivalence Relations:(0:00) Partitions:(9:22) Connecting Equivalence and Partitions:(14:09) Representatives:(27:04)
From playlist Axiomatic Set Theory

Univalent foundations and the equivalence principle - Benedikt Ahrens
Short Talks by Postdoctoral Members Benedikt Ahrens - September 21, 2015 http://www.math.ias.edu/calendar/event/88134/1442858400/1442859300 More videos on http://video.ias.edu
From playlist Short Talks by Postdoctoral Members