
a problem on irrational square roots
From playlist Common Core Standards - 7th Grade

An Alternative Look at Peg Solitaire
A video about peg solitaire, parity arguments, and biscuits. This video is for educational purposes. There is a lot of fun mathematics going on under the hood, including connections to linear programming, Diophantine equations and the mysteriously named Fredholm alternative. If you're in
From playlist Summer of Math Exposition 2 videos

Using long division to convert three sevenths to a decimal
From playlist Sevenths
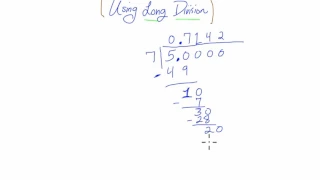
Using long division to convert five sevenths to a decimal
From playlist Sevenths

u09_l1_t3_we5 Identifying Rational Numbers
From playlist Developmental Math 2

MegaFavNumbers :- Evenly Primest Prime 232,222,222,222,233,333,333,222,222,222,222,222,322,222,223
#MegaFavNumber
From playlist MegaFavNumbers

an example that using properties of corresponding angles
From playlist Common Core Standards - 8th Grade

The Mathematical Problem with Music, and How to Solve It
There is a serious mathematical problem with the tuning of musical instruments. A problem that even Galileo, Newton, and Euler tried to solve. This video is about this problem and about some of the ways to tackle it. It starts from the basic physics of sound, proves mathematically why s
From playlist Summer of Math Exposition 2 videos

Metauni event #3: Lucas Cantor presents Music @ Metaverse
Lucas spoke on the emerging role of AI in music, and how this brings into focus some of the arbitrariness about the way we construct music, using the example of equal temperament. There was a very interesting question and discussion period after the talk, which among other things touched o
From playlist Metauni

Summer of Math Exposition 2022 - Mathematics and Music
"Better Late Than Never". I started taking Guitar lessons for the first time in my life in 2022. So I wanted to use Math to describe some musical concepts. This is a very rough draft and I wanted to share more but it's August 15th 2022. I created a slightly better video last year: h
From playlist Summer of Math Exposition 2 videos

How Pythagoras Broke Music (and how we kind of fixed it)
How does music work? What did an Ancient Greek philosopher have to do with it? Why did he keep drowning people? Discover the answers to these questions and more as we take a tour through musical tuning systems, examining how the power of mathematics has helped us build and rebuild our met
From playlist Mathematics

17.5 Transverse Standing Waves
This video covers Section 17.5 of Cutnell & Johnson Physics 10e, by David Young and Shane Stadler, published by John Wiley and Sons. The lecture is part of the course General Physics - Life Sciences I and II, taught by Dr. Boyd F. Edwards at Utah State University. This video was produced
From playlist Lecture 17B. Linear Superposition and Interference Phenomena

corresponding angles and straight lines - g5
using straight angles to find the values of different angles
From playlist Common Core Standards - 8th Grade

Determinism vs Free Will: Crash Course Philosophy #24
Do we really have free will? Today Hank explores possible answers to that question, explaining theories like libertarian free will and its counterpoint, hard determinism. -- Images via ThinkStock Produced in collaboration with PBS Digital Studios: http://youtube.com/pbsdigitalstudios C
From playlist Philosophy

Experts in Emotion 15.1a -- Jerome Kagan on Temperament
Experts in Emotion Series; Director: June Gruber, Yale University In this episode, you will learn about Temperament with Dr. Jerome Kagan from Harvard University. Dr. Kagan will share what first got him interested in this topic and highlight a few core themes in his research. Dr. Kagan w
From playlist Experts in Emotion Series with June Gruber

#MegaFavNumbers My favourite Number is 179 digits long!!!
#MegaFavNumbers sorry I had made mistakes about the prime factors. it was supposed to be 3×3×5×.... but I had taken it be 3×5×5×... and I have corrected below 31 980 599 086 523 546 548 147 351 491 272 676 211 458 715 997 231 784 732 063 781 637 489 066 745 716 387 150 725 397 533 911 7
From playlist MegaFavNumbers

Exact Values for Trigonometric Ratios
More resources available at www.misterwootube.com
From playlist Trigonometry

Temperament, heredity, and genes | Behavior | MCAT | Khan Academy
Created by Ryan Scott Patton. Watch the next lesson: https://www.khanacademy.org/test-prep/mcat/behavior/behavior-and-genetics/v/twin-studies-and-adoption-studies?utm_source=YT&utm_medium=Desc&utm_campaign=mcat Missed the previous lesson? https://www.khanacademy.org/test-prep/mcat/behavi
From playlist Behavior | MCAT | Khan Academy

