
Alessandro Chiodo - Towards a global mirror symmetry (Part 1)
Mirror symmetry is a phenomenon which inspired fundamental progress in a wide range of disciplines in mathematics and physics in the last twenty years; we will review here a number of results going from the enumerative geometry of curves to homological algebra. These advances justify the i
From playlist École d’été 2011 - Modules de courbes et théorie de Gromov-Witten

Watch more videos on http://www.brightstorm.com/math/geometry SUBSCRIBE FOR All OUR VIDEOS! https://www.youtube.com/subscription_center?add_user=brightstorm2 VISIT BRIGHTSTORM.com FOR TONS OF VIDEO TUTORIALS AND OTHER FEATURES! http://www.brightstorm.com/ LET'S CONNECT! Facebook ► https
From playlist Geometry

Reflecting a triangle over the y axis
👉 Learn how to reflect points and a figure over a line of symmetry. Sometimes the line of symmetry will be a random line or it can be represented by the x or y-axis. Either way when reflecting a point and or figure over the line of symmetry it is important to think of flipping the figure
From playlist Transformations
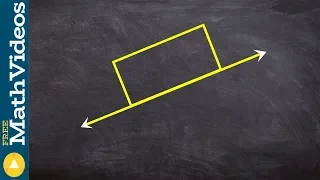
How to reflect a figure over a line of symmetry ex 1
👉 Learn how to reflect points and a figure over a line of symmetry. Sometimes the line of symmetry will be a random line or it can be represented by the x or y-axis. Either way when reflecting a point and or figure over the line of symmetry it is important to think of flipping the figure
From playlist Transformations

Reflecting a triangle over a line of symmetry
👉 Learn how to reflect points and a figure over a line of symmetry. Sometimes the line of symmetry will be a random line or it can be represented by the x or y-axis. Either way when reflecting a point and or figure over the line of symmetry it is important to think of flipping the figure
From playlist Transformations
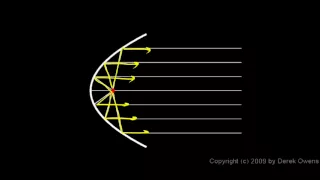
Physics 11.1.3a - Spherical and Parabolic Mirrors
Spherical and Parabolic mirrors. From the Physics course by Derek Owens. The distance learning class is available at www.derekowens.com
From playlist Physics - Reflection and Refraction

Learn how to reflect a figure over a line of symmetry
👉 Learn how to reflect points and a figure over a line of symmetry. Sometimes the line of symmetry will be a random line or it can be represented by the x or y-axis. Either way when reflecting a point and or figure over the line of symmetry it is important to think of flipping the figure
From playlist Transformations

Reflecting a figure over a line of symmetry when it is on both sides
👉 Learn how to reflect points and a figure over a line of symmetry. Sometimes the line of symmetry will be a random line or it can be represented by the x or y-axis. Either way when reflecting a point and or figure over the line of symmetry it is important to think of flipping the figure
From playlist Transformations
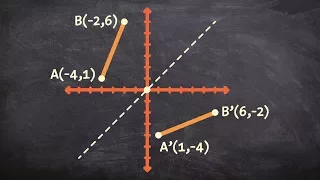
How to reflect a line segment over the y=x line
👉 Learn how to reflect points and a figure over a line of symmetry. Sometimes the line of symmetry will be a random line or it can be represented by the x or y-axis. Either way when reflecting a point and or figure over the line of symmetry it is important to think of flipping the figure
From playlist Transformations

Geometric Langlands and 3d Mirror Symmetry (Lecture 2) by Sam Raskin
Program Quantum Fields, Geometry and Representation Theory 2021 (ONLINE) ORGANIZERS: Aswin Balasubramanian (Rutgers University, USA), Indranil Biswas (TIFR, india), Jacques Distler (The University of Texas at Austin, USA), Chris Elliott (University of Massachusetts, USA) and Pranav Pandi
From playlist Quantum Fields, Geometry and Representation Theory 2021 (ONLINE)

Richard Rimanyi - Stable Envelopes, Bow Varieties, 3d Mirror Symmetry
There are many bridges connecting geometry with representation theory. A key notion in one of these connections, defined by Maulik-Okounkov, Okounkov, Aganagic-Okounkov, is the "stable envelope (class)". The stable envelope fits into the story of characteristic classes of singularities as
From playlist 2021 IHES Summer School - Enumerative Geometry, Physics and Representation Theory

The Quaternion Symmetry Group – Vi Hart
From playlist G4G11 Videos

MagLab Theory Winter School 2019: Bogdan A. Bernevig "Theory"
Topic: Topological Quantum Chemistry: Theory The National MagLab held it's seventh Theory Winter School in Tallahassee, FL from January 7th - 11th, 2019.
From playlist 2019 Theory Winter School

3D Gauge Theories: Vortices and Vertex Algebras (Lecture 2) by Tudor Dimofte
PROGRAM: VORTEX MODULI ORGANIZERS: Nuno Romão (University of Augsburg, Germany) and Sushmita Venugopalan (IMSc, India) DATE & TIME: 06 February 2023 to 17 February 2023 VENUE: Ramanujan Lecture Hall, ICTS Bengaluru For a long time, the vortex equations and their associated self-dual fie
From playlist Vortex Moduli - 2023

3d N = 4 Super-Yang-Mills on a Lattice by Arthur Lipstein
Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography DATE:27 January 2018 to 03 February 2018 VENUE:Ramanujan Lecture Hall, ICTS Bangalore The program "Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography" aims to
From playlist Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography

Supersymmetric Ground States of 3rd N=4 Theories on a Riemann surface by Heeyeon Kim
Program Quantum Fields, Geometry and Representation Theory 2021 (ONLINE) ORGANIZERS: Aswin Balasubramanian (Rutgers University, USA), Indranil Biswas (TIFR, india), Jacques Distler (The University of Texas at Austin, USA), Chris Elliott (University of Massachusetts, USA) and Pranav Pandi
From playlist Quantum Fields, Geometry and Representation Theory 2021 (ONLINE)

Viorica Patraucean: Mirror-symmetry in images and 3D shapes
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Mathematical Aspects of Computer Science

3D Gauge Theories: Vortices and Vertex Algebras (Lecture 2) by Tudor Dimofte
PROGRAM: VORTEX MODULI ORGANIZERS: Nuno Romão (University of Augsburg, Germany) and Sushmita Venugopalan (IMSc, India) DATE & TIME: 06 February 2023 to 17 February 2023 VENUE: Ramanujan Lecture Hall, ICTS Bengaluru For a long time, the vortex equations and their associated self-dual fie
From playlist Vortex Moduli - 2023

Geometric Langlands and 3d Mirror Symmetry (Lecture 1) by Sam Raskin
Program Quantum Fields, Geometry and Representation Theory 2021 (ONLINE) ORGANIZERS: Aswin Balasubramanian (Rutgers University, USA), Indranil Biswas (TIFR, india), Jacques Distler (The University of Texas at Austin, USA), Chris Elliott (University of Massachusetts, USA) and Pranav Pandi
From playlist Quantum Fields, Geometry and Representation Theory 2021 (ONLINE)

Reflecting a triangle over the y=x line
👉 Learn how to reflect points and a figure over a line of symmetry. Sometimes the line of symmetry will be a random line or it can be represented by the x or y-axis. Either way when reflecting a point and or figure over the line of symmetry it is important to think of flipping the figure
From playlist Transformations