
Multiplying two rational expressions
Learn how to multiply rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To multiply two rational expressions, we use the distributive property to multiply both numerators togethe
From playlist Multiply Rational Expressions (Trinomials) #Rational

Multiplying rational expressions
Learn how to multiply rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To multiply two rational expressions, we use the distributive property to multiply both numerators togethe
From playlist Multiply Rational Expressions (Trinomials) #Rational

Multiplying rational expressions
Learn how to multiply rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To multiply two rational expressions, we use the distributive property to multiply both numerators togethe
From playlist Add/Subtract Rational Expressions (Three) #Rational
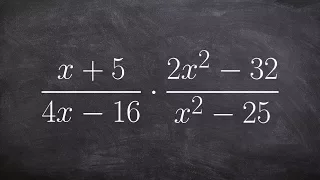
Multiplying rational expressions
Learn how to multiply rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To multiply two rational expressions, we use the distributive property to multiply both numerators togethe
From playlist Multiply Rational Expressions (Binomials) #Rational

Multiplying two rational expression when simplifying using the difference of two squares
Learn how to multiply rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To multiply two rational expressions, we use the distributive property to multiply both numerators togethe
From playlist Multiply Rational Expressions (Binomials) #Rational

Learn How to Compose Two Rational Functions and Simplify
Learn how to compose two functions where one or both of those functions is/are rational. To compose two functions means to express one of the functions as a function of the other function. This is done by replacing the input variable of one of the functions with the value of the second fun
From playlist How to Compose Two Functions (Rational) #Functions
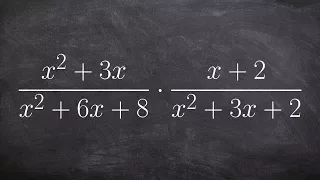
How to use factoring when multiplying two rational expressions
Learn how to multiply rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To multiply two rational expressions, we use the distributive property to multiply both numerators togethe
From playlist Multiply Rational Expressions (Trinomials) #Rational

Math tutorial for multiplying two rational expressions
Learn how to multiply rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To multiply two rational expressions, we use the distributive property to multiply both numerators togethe
From playlist Multiply Rational Expressions (Trinomials) #Rational

Yonatan Harpaz - New perspectives in hermitian K-theory III
For questions and discussions of the lecture please go to our discussion forum: https://www.uni-muenster.de/TopologyQA/index.php?qa=k%26l-conference This lecture is part of the event "New perspectives on K- and L-theory", 21-25 September 2020, hosted by Mathematics Münster: https://go.wwu
From playlist New perspectives on K- and L-theory

Multiplying rational expressions
Learn how to multiply rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To multiply two rational expressions, we use the distributive property to multiply both numerators togethe
From playlist Multiply Rational Expressions (Trinomials) #Rational

Teena Gerhardt - 3/3 Algebraic K-theory and Trace Methods
Algebraic K-theory is an invariant of rings and ring spectra which illustrates a fascinating interplay between algebra and topology. Defined using topological tools, this invariant has important applications to algebraic geometry, number theory, and geometric topology. One fruitful approac
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Lecture 6: HKR and the cotangent complex
In this video, we discuss the cotangent complex and give a proof of the HKR theorem (in its affine version) Feel free to post comments and questions at our public forum at https://www.uni-muenster.de/TopologyQA/index.php?qa=tc-lecture Homepage with further information: https://www.uni-m
From playlist Topological Cyclic Homology
Derived categories of cyclic covers and their branch divisors - Alexander Perry
Alexander Perry Harvard University April 29, 2015 Given a variety YY with a rectangular Lefschetz decomposition of its derived category, I will discuss an interesting relation between the derived categories of a cyclic cover of YY and its branch divisor. As examples, I will describe the c
From playlist Mathematics
Structures in the Floer theory of Symplectic Lie Groupoids - James Pascaleff
Symplectic Dynamics/Geometry Seminar Topic: Structures in the Floer theory of Symplectic Lie Groupoids Speaker: James Pascaleff Affiliation: University of Illinois, Urbana-Champaign Date: October 15, 2018 For more video please visit http://video.ias.edu
From playlist Mathematics

PROG2006: Haskell - lists, folds. Functors and applicatives: review. Intro to monads.
PROG2006 Advanced Programming Haskell: lists, folds. Functors and applicatives: review. Intro to monads.
From playlist PROG2006 - Programming

Sucharit Sarkar - Khovanov homotopy type
June 29, 2018 - This talk was part of the 2018 RTG mini-conference Low-dimensional topology and its interactions with symplectic geometry
From playlist 2018 RTG mini-conference on low-dimensional topology and its interactions with symplectic geometry II

Emily Cliff - Chiral algebras, factorization algebras,...
Chiral algebras, factorization algebras, and Borcherds' "singular commutative rings" approach to vertex algebras
From playlist Higher Structures in Holomorphic and Topological Field Theory

Lecture 12: Classifying topoi (Part 1)
This is the first of several talks on the subject of classifying topoi. I began with a brief reminder of the overall picture from the first talk, i.e. what are classifying topoi and why do we care (from the point of view of organising mathematics). Then I spent some time talking about tens
From playlist Topos theory seminar

Schemes 13: The functor of points
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. We discuss two themes in Grothendieck's work on schemes. The first one is that one should focus on morphisms of schemes rather than schemes. The second is that
From playlist Algebraic geometry II: Schemes

Ex: Function Values of a Function of Two Variables (Fraction)
This video provides an example of how to evaluate a function of two variables. Site: http://mathispower4u.com
From playlist Functions of Several Variables