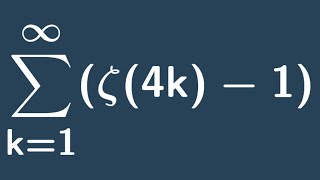
More identities involving the Riemann-Zeta function!
By applying some combinatorial tricks to an identity from https://youtu.be/2W2Ghi9idxM we are able to derive two identities involving the Riemann-Zeta function. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function

Some identities involving the Riemann-Zeta function.
After introducing the Riemann-Zeta function we derive a generating function for its values at positive even integers. This generating function is used to prove two sum identities. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function

Dirichlet Eta Function - Integral Representation
Today, we use an integral to derive one of the integral representations for the Dirichlet eta function. This representation is very similar to the Riemann zeta function, which explains why their respective infinite series definition is quite similar (with the eta function being an alte rna
From playlist Integrals

Understanding and computing the Riemann zeta function
In this video I explain Riemann's zeta function and the Riemann hypothesis. I also implement and algorithm to compute the return values - here's the Python script:https://gist.github.com/Nikolaj-K/996dba1ff1045d767b10d4d07b1b032f
From playlist Programming

More Riemann Zeta function identities!!
Building upon our previous video, we present three more Riemann zeta function identities. Video 1: https://youtu.be/2W2Ghi9idxM Video 2: https://www.youtube.com/watch?v=bRdGQKwusiE http://www.michael-penn.net https://www.researchgate.net/profile/Michael_Penn5 http://www.randolphcollege.e
From playlist The Riemann Zeta Function

Transcendental Functions 17 The Indefinite Integral of 1 over u du Example 1.mov
Example problems involving the integral of u to the power negative 1 du.
From playlist Transcendental Functions

Weil conjectures 1 Introduction
This talk is the first of a series of talks on the Weil conejctures. We recall properties of the Riemann zeta function, and describe how Artin used these to motivate the definition of the zeta function of a curve over a finite field. We then describe Weil's generalization of this to varie
From playlist Algebraic geometry: extra topics

Transcendental Functions 17 The Indefinite Integral of 1 over u du Example 2.mov
More example problems involving the integral of 1 over u, du.
From playlist Transcendental Functions

Mark Pollicott - Dynamical Zeta functions (Part 2)
Dynamical Zeta functions (Part 1) Licence: CC BY NC-ND 4.0
From playlist École d’été 2013 - Théorie des nombres et dynamique

Michal Eckstein: Asymptotic and exact expansion of spectral action
The asymptotic expansion of the spectral action at large energies is powerful tool for building models of fundamental interactions. For a suitable almost-commutative geometry it encodes the full lagrangian of the Standard Model minimally coupled to gravity. However, beyond the almost-commu
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Karlheinz Gröchenig: Gabor Analysis and its Mysteries (Lecture 2)
Due to technical problems the blackboard is not visible. The lecture was held within the framework of the Hausdorff Trimester Program Mathematics of Signal Processing. In Gabor analysis one studies the construction and properties of series expansions of functions with respect to a set of
From playlist HIM Lectures: Trimester Program "Mathematics of Signal Processing"

Mark Pollicott - Dynamical Zeta functions (Part 3)
Dynamical Zeta functions (Part 1) Licence: CC BY NC-ND 4.0
From playlist École d’été 2013 - Théorie des nombres et dynamique

Monotonicity of the Riemann zeta function and related functions - P Zvengrowski [2012]
General Mathematics Seminar of the St. Petersburg Division of Steklov Institute of Mathematics, Russian Academy of Sciences May 17, 2012 14:00, St. Petersburg, POMI, room 311 (27 Fontanka) Monotonicity of the Riemann zeta function and related functions P. Zvengrowski University o
From playlist Number Theory

Andras Vasy - Microlocal analysis and wave propagation (Part 2)
In these lectures I will explain the basics of microlocal analysis, emphasizing non-elliptic problems, such as wave propagation, both on manifolds without boundary, and on manifolds with boundary. In the latter case there is no « standard » algebra of differential, or pseudodifferential,
From playlist Ecole d'été 2014 - Analyse asymptotique en relativité générale

Yiannis Sakellaridis - 2/2 Local and Global Questions “Beyond Endoscopy”
The near-completion of the program of endoscopy poses the question of what lies next. These talks will take a broad view of ideas beyond the program of endoscopy, highlighting the connections among them, and emphasizing the relationship between local and global aspects. Central among thos
From playlist 2022 Summer School on the Langlands program

Alexandre Sukhov - J-complex curves: some applications (Part 3)
We will focus in our lectures on the following : 1. J-complex discs in almost complex manifolds : general properties. Linearization and compactness. Gromov’s method : the Fredholm alternative for the d-bar operator. Attaching a complex disc to a Lagrangian manifold. Application : exotic sy
From playlist École d’été 2012 - Feuilletages, Courbes pseudoholomorphes, Applications

Julie Rowlett: A Polyakov formula for sectors
Abstract: Polyakov's formula expresses a difference of zeta-regularized determinants of Laplace operators, an anomaly of global quantities, in terms of simple local quantities. Such a formula is well known in the case of closed surfaces (Osgood, Philips, & Sarnak 1988) and surfaces with sm
From playlist Women at CIRM

Calderon problem (Lecture 1) by Venkateswaran P Krishnan
DISCUSSION MEETING WORKSHOP ON INVERSE PROBLEMS AND RELATED TOPICS (ONLINE) ORGANIZERS: Rakesh (University of Delaware, USA) and Venkateswaran P Krishnan (TIFR-CAM, India) DATE: 25 October 2021 to 29 October 2021 VENUE: Online This week-long program will consist of several lectures by
From playlist Workshop on Inverse Problems and Related Topics (Online)

[BOURBAKI 2019] The Riemann zeta function in short intervals - Harper - 30/03/19
Adam HARPER The Riemann zeta function in short intervals A classical idea for studying the behaviour of complicated functions, like the Riemann zeta function ζ(s), is to investigate averages of them. For example, the integrals over T ≤ t ≤ 2T of various powers of ζ(1/2 + it), sometimes m
From playlist BOURBAKI - 2019

The Field With One Element and The Riemann Hypothesis (Full Video)
A crash course of Deninger's program to prove the Riemann Hypothesis using a cohomological interpretation of the Riemann Zeta Function. You can Deninger talk about this in more detail here: http://swc.math.arizona.edu/dls/ Leave some comments!
From playlist Riemann Hypothesis