Zero lower bound

Interest rates

The Zero Lower Bound (ZLB) or Zero Nominal Lower Bound (ZNLB) is a macroeconomic problem that occurs when the short-term nominal interest rate is at or near zero, causing a liquidity trap and limiting the central bank's capacity to stimulate economic growth. The root cause of the ZLB is the issuance of paper currency by governments, effectively guaranteeing a zero nominal interest rate and acting as an interest rate floor. Governments cannot encourage spending by lowering interest rates, because people would simply hold cash instead. Miles Kimball suggested that a modern economy either fully relying on electronic money or defining electronic money as the unit of account could eliminate the ZLB. Even without such measures, however, several central banks are able to reduce interest rates below zero; for example, the Czech National Bank estimates that the lower limit on its interest rate is below -1%. The problem of the ZLB returned to prominence with Japan's experience during the 90's, and more recently with the subprime crisis. The belief that monetary policy under the ZLB was effective in promoting economy growth has been critiqued by Paul Krugman, , and Michael Woodford among others. Milton Friedman, on the other hand, argued that a zero nominal interest rate presents no problem for monetary policy. According to Friedman, a central bank can increase the monetary base even if the interest rate vanishes; it only needs to continue buying bonds. Friedman also coined the term "helicopter drops" to illustrate how central banks could always generate spending and inflation. Friedman used the example of a helicopter flying over a town dropping dollar bills from the sky, which households then gathered in perfectly equal shares. Economists have argued that real-world versions of this idea would work at the zero lower bound. Typically, helicopter drops have been interpreted as involving the central bank directly financing the budget deficit. The economist Willem Buiter has argued that helicopter drops can always raise demand and inflation. Following the repeated struggles of the European Central Bank to revive the Eurozone economy and meet its inflation objective, a number of economists have taken a more literal interpretation of Friedman's parable and suggested that the European Central Bank should transfer cash directly to households. (Wikipedia).

Upper Bound

Upper and Lower Bound In this video, I define what it means for a set to be bounded above and bounded below. This will be useful in our definition of inf and sup. Check out my Real Numbers Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmCZggpJZvUXnUzaw7fHCtoh

From playlist Real Numbers

Calculating With Upper & Lower Bounds | Number | Maths | FuseSchool

Calculating With Upper & Lower Bounds | Number | Maths | FuseSchool In this video we are going to look at how to calculate with upper and lower bounds. To find the upper bound of an addition or of an area, you would want to multiply the upper bounds of both measurements, as this would g

From playlist MATHS: Numbers

Math 101 091517 Introduction to Analysis 07 Consequences of Completeness

Least upper bound axiom implies a "greatest lower bound 'axiom'": that any set bounded below has a greatest lower bound. Archimedean Property of R.

From playlist Course 6: Introduction to Analysis (Fall 2017)

Math 101 091317 Introduction to Analysis 06 Introduction to the Least Upper Bound Axiom

Definition of the maximum (minimum) of a set. Existence of maximum and minimum for finite sets. Definitions: upper bound of a set; bounded above; lower bound; bounded below; bounded. Supremum (least upper bound); infimum (greatest lower bound). Statement of Least Upper Bound Axiom (com

From playlist Course 6: Introduction to Analysis (Fall 2017)

GCSE Upper and Lower Bounds Introduction Measures of Accuracy

www.m4ths.com GCSE and A Level Worksheets, videos and helpbooks. Full course help for Foundation and Higher GCSE 9-1 Maths All content created by Steve Blades

From playlist GCSE Upper and Lower Bounds

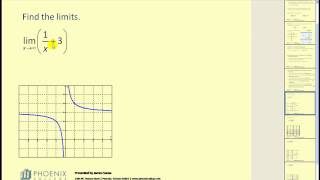
Introduction to Limits at Infinity (Part 1)

This video introduces limits at infinity. https://mathispower4u.com

From playlist Limits at Infinity and Special Limits

Calculus 1.5.1 Determine Infinite Limits

From playlist Calculus I (Entire Course)

Limits At Infinity

http://mathispower4u.wordpress.com/

From playlist Limits

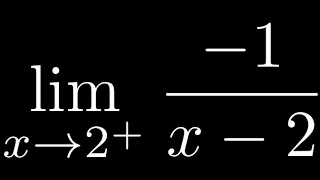
How to Compute a One Sided limit as x approaches from the right

In this video I will show you How to Compute a One Sided limit as x approaches from the right.

From playlist One-sided Limits

Math 131 090516 Lecture #02 LUB property, Ordered Fields

Least Upper Bound Property and Greatest Lower Bound Property; Fields; Properties of Fields; Ordered Fields and properties; description of the real numbers (ordered field with LUB property containing rational numbers as subfield); Archimedean property #fields #orderedfields #leastupperboun

From playlist Course 7: (Rudin's) Principles of Mathematical Analysis

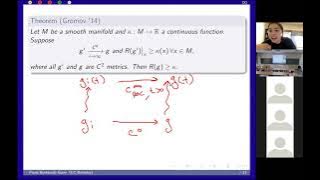
P. Burkhardt-Pointwise lower scalar curvature bounds for C0 metrics via regularizing Ricci flow (vt)

We propose a class of local definitions of weak lower scalar curvature bounds that is well defined for C0 metrics. We show the following: that our definitions are stable under greater-than-second-order perturbation of the metric, that there exists a reasonable notion of a Ricci flow starti

From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

P. Burkhardt-Pointwise lower scalar curvature bounds for C0 metrics via regularizing Ricci flow

From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

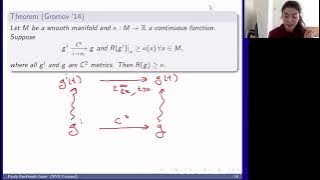
Paula Burkhardt-Guim - Lower scalar curvature bounds for $C^0$ metrics: a Ricci flow approach

We describe some recent work that has been done to generalize the notion of lower scalar curvature bounds to C^0 metrics, including a localized Ricci flow approach. In particular, we show the following: that there is a Ricci flow definition which is stable under greater-than-second-order p

From playlist Not Only Scalar Curvature Seminar

Math 131 Fall 2018 091018

From playlist Course 7: (Rudin's) Principles of Mathematical Analysis (Fall 2018)

Math 131 Fall 2018 091218

From playlist Course 7: (Rudin's) Principles of Mathematical Analysis (Fall 2018)

Using Bounds to Calculate Further Bounds

"Use lower and upper bounds within calculations to calculate a further lower/upper bound."

From playlist Number: Rounding & Estimation

Math 101 Introduction to Analysis 091815: Least Upper Bound Axiom

The least upper bound axiom. Maximum and minimum of a set of real numbers. Upper bound; lower bound; bounded set. Least upper bound; greatest lower bound.

From playlist Course 6: Introduction to Analysis

Bounds - Upper and Lower Bound Calculations | Grade 7-9 Maths Series | GCSE Maths Tutor

A video revising the techniques and strategies for looking at bounds calculations (Higher Only). This video is part of the Bounds module in GCSE maths, see my other videos below to continue with the series. These are the calculators that I recommend 💎 Casio fx-83GTX Scientific Calculat

From playlist GCSE Maths Videos

Lecture 8 | Convex Optimization I (Stanford)

Professor Stephen Boyd, of the Stanford University Electrical Engineering department, lectures on duality in the realm of electrical engineering and how it is utilized in convex optimization for the course, Convex Optimization I (EE 364A). Convex Optimization I concentrates on recognizi

From playlist Lecture Collection | Convex Optimization

Least Upper Bound Property

Least Upper Bound Property In this video, I state the least upper bound property and explain what makes the real numbers so much better than the rational numbers. It's called Real Analysis after all! Check out my Real Numbers Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmCZ

From playlist Real Numbers

Zero lower bound

Related pages