
Projection Theorem | Special Case of the Wigner–Eckart Theorem
The projection theorem is a special case of the Wigner–Eckart theorem, which generally involves spherical tensor operators. If we consider one example of a spherical tensor operator, a rank-1 spherical tensor, we can derive a powerful theorem, which states that expectation values of vector
From playlist Quantum Mechanics, Quantum Field Theory

Representation theory: Frobenius groups
We recall the definition of a Frobenius group as a transitive permutation group such that any element fixing two points is the identity. Then we prove Frobenius's theorem that the identity together with the elements fixing no points is a normal subgroup. The proof uses induced representati
From playlist Representation theory

RT4.2. Schur's Lemma (Expanded)
Representation Theory: We introduce Schur's Lemma for irreducible representations and apply it to our previous constructions. In particular, we identify Hom(V,V) with invariant sesquilinear forms on V when (pi, V) is unitary. Course materials, including problem sets and solutions, availa
From playlist Representation Theory

Representation theory: Introduction
This lecture is an introduction to representation theory of finite groups. We define linear and permutation representations, and give some examples for the icosahedral group. We then discuss the problem of writing a representation as a sum of smaller ones, which leads to the concept of irr
From playlist Representation theory
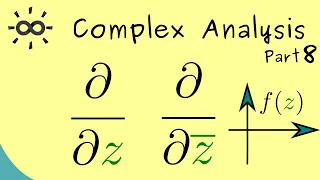
Complex Analysis - Part 8 - Wirtinger Derivatives
Support the channel on Steady: https://steadyhq.com/en/brightsideofmaths Or support me via PayPal: https://paypal.me/brightmaths Or via Ko-fi: https://ko-fi.com/thebrightsideofmathematics Or via Patreon: https://www.patreon.com/bsom Or via other methods: https://thebrightsideofmathematics.
From playlist Complex Analysis

Jeffrey Achter, Equidistribution counts abelian varieties
VaNTAGe Seminar, February 22, 2022 License: CC-BY-NC-SA Links to some of the papers mentioned in this talk are listed below. Sutherland: https://arxiv.org/abs/1604.01256 Gekeler: https://academic.oup.com/imrn/article/2003/37/1999/863196 Job Rauch: https://www.universiteitleiden.nl/binar
From playlist Curves and abelian varieties over finite fields

RT8.3. Finite Groups: Projection to Irreducibles
Representation Theory: Having classified irreducibles in terms of characters, we adapt the methods of the finite abelian case to define projection operators onto irreducible types. Techniques include convolution and weighted averages of representations. At the end, we state and prove th
From playlist Representation Theory

How to find the position function given the acceleration function
👉 Learn how to approximate the integral of a function using the Reimann sum approximation. Reimann sum is an approximation of the area under a curve or between two curves by dividing it into multiple simple shapes like rectangles and trapezoids. In using the Reimann sum to approximate the
From playlist Riemann Sum Approximation

RT6. Representations on Function Spaces
Representation Theory: We note how to transfer a group action of a group G on a set X to a group action on F(X), the functions on X. Because F(X) is a vector space, we obtain a representation of the group, and we can apply previous techniques. In particular, the group acts on itself in
From playlist Representation Theory

Xiadong Li: Phase Retrieval from Convex to Nonconvex Methods
Xiadong Li: Phase Retrieval from Convex to Nonconvex Methods Abstract: In phase retrieval, one aims to recover a signal from magnitude measurements. In the literature, an effective SDP algorithm, referred to as PhaseLift, was proposed with numerical success as well as strong theoretical g
From playlist HIM Lectures: Trimester Program "Mathematics of Signal Processing"
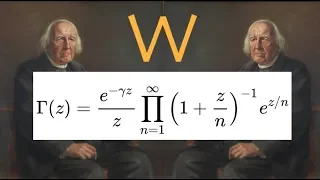
Infinite products & the Weierstrass factorization theorem
In this video we're going to explain the Weierstrass factorization theorem, giving rise to infinite product representations of functions. Classical examples are that of the Gamma function or the sine function. https://en.wikipedia.org/wiki/Weierstrass_factorization_theorem https://en.wiki
From playlist Programming

Frédéric Hérau: A Korn Wirtinger inequality
The lecture was held within the of the Hausdorff Junior Trimester Program: Kinetic Theory Abstract: In kinetic theory or in other fields, some control of the gradient by the symmetric gradient of the macroscopic velocity of a system of particle may be necessary, since only the second qua
From playlist HIM Lectures: Junior Trimester Program "Kinetic Theory"

Daniel Pomerleano: Degenerations from Floer cohomology
The lecture was held within the framework of the Hausdorff Trimester Program: Symplectic Geometry and Representation Theory. Abstract: I will explain how, under suitable hypotheses, one can construct a flat degeneration from the symplectic cohomology of log Calabi-Yau varieties to the Sta
From playlist HIM Lectures: Trimester Program "Symplectic Geometry and Representation Theory"

Dipendra Prasad - Branching laws: homological aspects
By this time in the summer school, the audience will have seen the question about decomposing a representation of a group when restricted to a subgroup which is referred to as the branching law. In this lecture, we focus attention on homological aspects of the branching law. The lecture
From playlist 2022 Summer School on the Langlands program

Ext-analogues of Branching laws – Dipendra Prasad – ICM2018
Lie Theory and Generalizations Invited Lecture 7.5 Ext-analogues of Branching laws Dipendra Prasad Abstract: We consider the Ext-analogues of branching laws for representations of a group to its subgroups in the context of p-adic groups. ICM 2018 – International Congress of Mathematic
From playlist Lie Theory and Generalizations

Branching laws: homological aspects - Dipendra Prasad
Joint IAS/Princeton University Number Theory Seminar Topic: Branching laws: homological aspects Speaker: Dipendra Prasad Affiliation: Indian Institute of Technology Date: May 19, 2022 This lecture will partly survey branching laws for real and p-adic groups which often is related to peri
From playlist Mathematics

Modular Representation Theory: Week Two
Presented by Chris Hone.
From playlist Modular Representation Theory

Quiver moduli and applications, Markus Reineke (Bochum), Lecture 3
Quiver moduli spaces are algebraic varieties encoding the continuous parameters of linear algebra type classification problems. In recent years their topological and geometric properties have been explored, and applications to, among others, Donaldson-Thomas and Gromov-Witten theory have
From playlist Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum)

Representation theory: Induced representations
We define induced representations of finite groups in two ways as either left or right adjoints of the restriction functor. We calculate the character of an induced representation, and give an example of an induced representation of S3.
From playlist Representation theory

On the Mod p Cohomology for GL_2 (I) by Haoran Wang
Program Recent developments around p-adic modular forms (ONLINE) ORGANIZERS: Debargha Banerjee (IISER Pune, India) and Denis Benois (University of Bordeaux, France) DATE: 30 November 2020 to 04 December 2020 VENUE: Online This is a follow up of the conference organized last year arou
From playlist Recent Developments Around P-adic Modular Forms (Online)