
k-NN 4: which distance function?
[http://bit.ly/k-NN] The nearest-neighbour algorithm is sensitive to the choice of distance function. Euclidean distance (L2) is a common choice, but it may lead to sub-optimal performance. We discuss Minkowski (p-norm) distance functions, which generalise the Euclidean distance, and can a
From playlist Nearest Neighbour Methods

This video show how to use the distance formula to determine the distance between two points. It also shows how it is derived from the Pythagorean theorem. http://mathispower4u.yolasite.com/
From playlist Using the Distance Formula / Midpoint Formula

How to Find the Distance Between Two Points - How to Use the Distance Formula
This tutorial shows how the distance formula is used to find the distance between two points in a x y coordinate system. Join this channel to get access to perks: https://www.youtube.com/channel/UCn2SbZWi4yTkmPUj5wnbfoA/join :)
From playlist Pythagorean Theorem and the Distance Formula
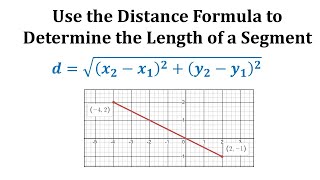
Example: Determine the Distance Between Two Points
This video shows an example of determining the length of a segment on the coordinate plane by using the distance formula. Complete Video List: http://www.mathispower4u.yolasite.com or http://www.mathispower4u.wordpress.com
From playlist Using the Distance Formula / Midpoint Formula
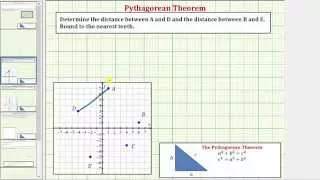
Ex: Determine the Distance Between Two Points Using the Pythagorean Theorem
This video explains how to determine the distance between two points on the coordinate plane using the Pythagorean Theorem. http://mathispower4u.com
From playlist Using the Pythagorean Theorem

Distance Formula given two points
In this video, we review how to calculate the distance if we are given the value of two points
From playlist Geometry

Distance as a function -- Proofs
This lecture is on Introduction to Higher Mathematics (Proofs). For more see http://calculus123.com.
From playlist Proofs

Topology and the Electromagnetic Responses of Quantum Materials by Joel E. Moore
ICTS at Ten ORGANIZERS: Rajesh Gopakumar and Spenta R. Wadia DATE: 04 January 2018 to 06 January 2018 VENUE: International Centre for Theoretical Sciences, Bengaluru This is the tenth year of ICTS-TIFR since it came into existence on 2nd August 2007. ICTS has now grown to have more tha
From playlist ICTS at Ten

Differential Isomorphism and Equivalence of Algebraic Varieties Board at 49:35 Sum_i=1^N 2/(x-phi_i(y,t))^2
From playlist Fall 2017

D. Prandri - Weyl law for singular Riemannian manifolds
In this talk we present recent results on the asymptotic growth of eigenvalues of the Laplace-Beltrami operator on singular Riemannian manifolds, where all geometrical invariants appearing in classical spectral asymptotics are unbounded, and the total volume can be infinite. Under suitable
From playlist Journées Sous-Riemanniennes 2018

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys The Distance Formula
From playlist College Algebra

Transport in topological junctions by Krishnendu Sengupta
Program The 2nd Asia Pacific Workshop on Quantum Magnetism ORGANIZERS: Subhro Bhattacharjee, Gang Chen, Zenji Hiroi, Ying-Jer Kao, SungBin Lee, Arnab Sen and Nic Shannon DATE: 29 November 2018 to 07 December 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Frustrated quantum magne
From playlist The 2nd Asia Pacific Workshop on Quantum Magnetism

David Zywina, Computing Sato-Tate and monodromy groups.
VaNTAGe seminar on May 5, 2020. License: CC-BY-NC-SA Closed captions provided by Jun Bo Lau.
From playlist The Sato-Tate conjecture for abelian varieties
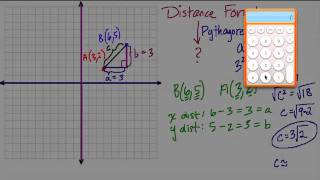
An overview of the distance formula and how it connects to the pythagorean theorem
From playlist Geometry

Weyl Law in Liouville Quantum Gravity - Nathanaël Berestycki
Probability Seminar Topic: Weyl Law in Liouville Quantum Gravity Speaker: Nathanaël Berestycki Affiliation: University of Vienna Date: February 3, 2023 Can you hear the shape of LQG? We obtain a Weyl law for the eigenvalues of Liouville Brownian motion: the n-th eigenvalue grows linearly
From playlist Mathematics

Andreas Bernig: Intrinsic volumes on pseudo-Riemannian manifolds
The intrinsic volumes in Euclidean space can be defined via Steiner’s tube formula and were characterized by Hadwiger as the unique continuous, translation and rotation invariant valuations. By the Weyl principle, their extension to Riemannian manifolds behaves naturally under isometric em
From playlist Workshop: High dimensional measures: geometric and probabilistic aspects

Peter Jung: Some Aspects of Weyl Heisenberg Signal Design in Wireless Communication
Peter Jung: Some Aspects of Weyl Heisenberg Signal Design in Wireless Communication Abstract: Signal design using the structure of the Weyl-Heisenberg group is an important topic in several engineering disciplines. This includes, for example, pulse shaping for robust multicarrier transmis
From playlist HIM Lectures: Trimester Program "Mathematics of Signal Processing"

High Dimensional Expansion and Error Correcting Codes - Irit Dinur
Hermann Weyl Lectures Topic: High Dimensional Expansion and Error Correcting Codes Speaker: Irit Dinur Affiliation: Weizmann Institute of Science; Visiting Professor, School of Mathematics Date: November 19, 2019 For more video please visit http://video.ias.edu
From playlist Hermann Weyl Lectures

Pre-Calculus - Using the Distance Formula
This video explains how to use the distance formula on two points. Time is also taken to explain the exact answer it returns vs the decimal approximation which can be a bit more useful. For kore videos visit http://www.mysecretmathtutor.com
From playlist Pre-Calculus - Linear Functions

Recent developments in Quantum Magnetism by Gang Chen
Program The 2nd Asia Pacific Workshop on Quantum Magnetism ORGANIZERS: Subhro Bhattacharjee, Gang Chen, Zenji Hiroi, Ying-Jer Kao, SungBin Lee, Arnab Sen and Nic Shannon DATE: 29 November 2018 to 07 December 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Frustrated quantum magne
From playlist The 2nd Asia Pacific Workshop on Quantum Magnetism