
C49 Example problem solving a system of linear DEs Part 1
Solving an example problem of a system of linear differential equations, where one of the equations is not homogeneous. It's a long problem, so this is only part 1.
From playlist Differential Equations

C50 Example problem solving a system of linear DEs Part 2
Part 2 of the prvious example problem, solving a system of linear differential equations, where one of the equations is non-homogeneous.
From playlist Differential Equations

Laplace's equation: Why are solutions unique?
Free ebook https://bookboon.com/en/partial-differential-equations-ebook Why does Laplace's equation have, at most, one solution and how is this information useful? Such ideas arise in the study of partial differential equations.
From playlist Partial differential equations
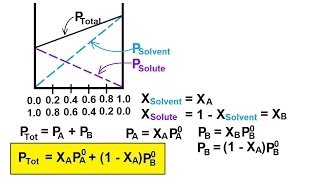
Chemistry - Solutions (30 of 53) Colligative Properties- Vapor Pressure & Volatile Solute: Ideal
Visit http://ilectureonline.com for more math and science lectures! In this video I find the equation of an ideal case of vapor pressure and volatile solute.
From playlist CHEMISTRY 19 SOLUTIONS

C36 Example problem solving a Cauchy Euler equation
An example problem of a homogeneous, Cauchy-Euler equation, with constant coefficients.
From playlist Differential Equations

B06 Example problem with separable variables
Solving a differential equation by separating the variables.
From playlist Differential Equations

B23 Example problem solving for a homogeneous DE
The first substitution changes a DE in differential form that could not otherwise be solved (it is not exact, nor can it be changed into an exact equation by using an integrating factor) into a DE in which separation of variables can be applied. Make sure the DE is homogeneous, though.
From playlist Differential Equations

5 Groundbreaking Women in Engineering
This episode was produced in collaboration with and sponsored by Emerson. Click here to learn more about their We Love STEM initiative: https://www.emerson.com/welovestem?cm_mmc=SciShow-_-Video-_-Youtube-_-WomenInSTEM2019 #WeLoveSTEM #STEM #Engineering #WomenInSTEM After many years of qu
From playlist Uploads

29C3: Best of ... Verfassungsschutz (DE)
Speaker: Anne Roth Der Verfassungsschutz schützt die Verfassung so wie Zitronenfalter Zitronen falten. Verfassungsschutzskandale gibt es nicht erst seit der Entdeckung des NSU vor einem Jahr. Vorgestellt werden: sie Affaire Traube, der Schmücker-Prozess, das Celler Loch, die Vulkan-Affai
From playlist 29C3: Not my department

Mixture Problems in Linear Differential Equations (Differential Equations 19)
https://www.patreon.com/ProfessorLeonard How to solve Mixture Problems with Linear First Order Differential Equations.
From playlist Differential Equations

ElixirConf 2015 - Interoperability in Elixir: Dealing With the World Outside of the Beam
by James Smith Interoperability in Elixir Dealing With the World Outside of the Beam Ports, Nifs, and Interfaces, Oh my! Elixir is an incredibly powerful language that sits on top of the battle tested and reliable Erlang ecosystem. This power is a big reason I am excited about building app
From playlist ElixirConf 2015

There's more over on Veritasium! "What is NOT Random?": https://www.youtube.com/watch?v=sMb00lz-IfE SOURCES AND MORE BELOW! My twitter: https://twitter.com/tweetsauce My instagram: http://instagram.com/electricpants Generate random numbers using atmospheric noise: http://www.random.org/
From playlist Knowledge

Supercomputers Solve Case of Missing Galaxies
More Info: http://www.caltech.edu/news/recreating-our-galaxy-supercomputer-51995 Caltech Associate Professor of Theoretical Astrophysics Phil Hopkins and Carnegie-Caltech Research Fellow Andrew Wetzel use massive supercomputers to build the most detailed and realistic simulation of galaxy
From playlist Our Research

The Baryon Content of Isolated Dwarf Galaxies - Marla Geha
Joint IAS/Princeton University Astrophysics Colloquium Tuesday, October 20, 2015 http://www.sns.ias.edu/~seminar/colloquia.shtml Environment plays a major in role in the evolution of galaxies. This is particularly true of low mass dwarf galaxies where more massive galaxies dramatically a
From playlist Joint IAS/PU Astrophysics Colloquium

When Iceland Defeated Britain: The Cod Wars (Short Animated Documentary)
Twitter: https://twitter.com/Tenminhistory Patreon: https://www.patreon.com/user?u=4973164 Merch: https://teespring.com/stores/history-matters-store-2 Special Thanks to the following Patrons for their support on Patreon: Alen Richard Wolfe Chris Fatta Kevin Sanders Daniel Lambert Stefan
From playlist The Cold War (1945-1991)

Jessi answers viewer questions about animal escapes, parrot attacks, first shows, and the hardest animal to care for. Link to Positive Reinforcement video: https://youtu.be/3YY4Mhp3ZFA Link to Teeth Trimming video: https://youtu.be/wWBl4CBLIng Our Video Sponsors: Scott Tengesdal Alice C
From playlist Ask Jessi

Why Did Britain Refuse to Annex Malta? (Short Animated Documentary)
In 1955 the Maltese government asked to be incorporated into the United Kingdom as its fifth constituent nation. As you'll be aware, that never happened and Britain refused to annex the Mediterranean island. But why? Well, find out by watching this short and simple animated documentary. T
From playlist The Cold War (1945-1991)

The Romanian Revolution: Explained (Short Animated Documentary)
In 1989, a wave of revolution swept across Eastern Europe, disrupting the Communist governments of Poland, East Germany, Czechoslovakia, Bulgaria, Hungary and of course, Romania. But how did the Romanian Revolution play out and why couldn't Nicolae Ceaușescu or the authorities stop it like
From playlist The Cold War (1945-1991)

B07 Example problem with separable variables
Solving a differential equation by separating the variables.
From playlist Differential Equations
