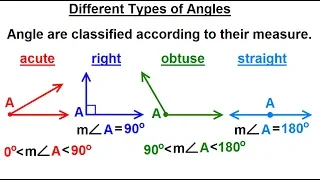
Geometry - Ch. 1: Basic Concepts (18 of 49) What are the Different Types of Angles?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain the definition of an and show how to recognize an acute, right, obtuse, and straight angle. Next video in this series can be seen at: https://youtu.be/QAui1XjG05Y
From playlist THE "WHAT IS" PLAYLIST

Learn all about angles. An angle is a figure formed by two rays sharing a common endpoint. An angle can be classified as acute, right, obtuse, straight or refrex. An acute angle is an angle which measures less than 90 degrees. A right angle measures 90 degrees. An obtuse angle measures mor
From playlist Learn all about basics of Angles #Geometry

How do we classify the angles - Obtuse, straight, acute, right
Learn all about angles. An angle is a figure formed by two rays sharing a common endpoint. An angle can be classified as acute, right, obtuse, straight or refrex. An acute angle is an angle which measures less than 90 degrees. A right angle measures 90 degrees. An obtuse angle measures mor
From playlist Learn all about basics of Angles #Geometry

Classifying Functions & Relations (2 of 2: 1-to-Many, Many-to-Many)
More resources available at www.misterwootube.com
From playlist Working with Functions

How to label the sides of an angle
Learn all about angles. An angle is a figure formed by two rays sharing a common endpoint. An angle can be classified as acute, right, obtuse, straight or refrex. An acute angle is an angle which measures less than 90 degrees. A right angle measures 90 degrees. An obtuse angle measures mor
From playlist Learn all about basics of Angles #Geometry

The Triangle Inequalities (3 of 3: Difference of Complex Numbers)
More resources available at www.misterwootube.com
From playlist Complex Numbers

Equivariantization and de-equivariantization - Shotaro Makisumi
Geometric and Modular Representation Theory Seminar Topic: Equivariantization and de-equivariantization Speaker: Shotaro Makisumi Affiliation: Columbia University; Member, School of Mathematics Date: February 10, 2021 For more video please visit http://video.ias.edu
From playlist Seminar on Geometric and Modular Representation Theory

Partially wrapped Fukaya categories of symmetric products of marked disks, Gustavo Jasso
Partially wrapped Fukaya categories of symmetric products of marked surfaces were in- troduced by Auroux so as to give a symplecto-geometric intepretation of the bordered Heegaard-Floer homology of Lipshitz, Ozsv ́ath and Thurston. In this talk, I will explain the equivalence between the p
From playlist Winter School on “Connections between representation Winter School on “Connections between representation theory and geometry"

Clark Barwick - 1/3 Exodromy for ℓ-adic Sheaves
In joint work with Saul Glasman and Peter Haine, we proved that the derived ∞-category of constructible ℓ-adic sheaves ’is’ the ∞-category of continuous functors from an explicitly defined 1-category to the ∞-category of perfect complexes over ℚℓ. In this series of talks, I want to offer s
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Clark Barwick - 2/3 Exodromy for ℓ-adic Sheaves
In joint work with Saul Glasman and Peter Haine, we proved that the derived ∞-category of constructible ℓ-adic sheaves ’is’ the ∞-category of continuous functors from an explicitly defined 1-category to the ∞-category of perfect complexes over ℚℓ. In this series of talks, I want to offer s
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

D. Gaitsgory - "fundamental local equivalence" for quantum geometric Langlands
The key role in the usual geometric Langlands is played by the geometric Satake equivalence, which says that the category of spherical perverse sheaves on the affine Grassmannian Gr_G of the group G is equivalent to the category Rep(G^L) of algebraic representations of the Langlands dual G
From playlist Arithmetic and Algebraic Geometry: A conference in honor of Ofer Gabber on the occasion of his 60th birthday

Hecke category via derived convolution formalism - Dima Arinkin
Geometric and Modular Representation Theory Seminar Topic: Hecke category via derived convolution formalism Speaker: Dima Arinkin Affiliation: University of Wisconsin–Madison Date: December 16, 2020 For more video please visit http://video.ias.edu
From playlist Seminar on Geometric and Modular Representation Theory

Marc Levine - "The Motivic Fundamental Group"
Research lecture at the Worldwide Center of Mathematics.
From playlist Center of Math Research: the Worldwide Lecture Seminar Series

Shadows of Computation - Lecture 1 - Making subtle ideas apparent
Welcome to Shadows of Computation, an online course taught by Will Troiani and Billy Snikkers, covering the foundations of category theory and how it is used by computer scientists to abstract computing systems to reveal their intrinsic mathematical properties. In the first lecture Will in
From playlist Shadows of Computation

Sucharit Sarkar - Khovanov homotopy type
June 29, 2018 - This talk was part of the 2018 RTG mini-conference Low-dimensional topology and its interactions with symplectic geometry
From playlist 2018 RTG mini-conference on low-dimensional topology and its interactions with symplectic geometry II

Higher Algebra 9: Symmetric monoidal infinity categories
In this video, we introduce the notion of a symmetric monoidal infinity categories and give some examples. Feel free to post comments and questions at our public forum at https://www.uni-muenster.de/TopologyQA/index.php?qa=tc-lecture Homepage with further information: https://www.uni-mu
From playlist Higher Algebra

More resources available at www.misterwootube.com
From playlist Data Collection & Representation


