
Yusuke Kobayashi: A weighted linear matroid parity algorithm
The lecture was held within the framework of the follow-up workshop to the Hausdorff Trimester Program: Combinatorial Optimization. Abstract: The matroid parity (or matroid matching) problem, introduced as a common generalization of matching and matroid intersection problems, is so gener
From playlist Follow-Up-Workshop "Combinatorial Optimization"

Working with Matrices in Matlab
This tutorial shows how to define and manipulate matrices in Matlab. Topics and timestamps: 0:00 – Introduction 1:19 – Defining a matrix 6:59 – Matrix multiplication (both standard and elementwise) 14:19 – Extracting submatrices 18:16 – Transpose 19:12 – Concatenation 21:57 – Creating l
From playlist Working with Matlab

Joseph Bonin: Delta-matroids as subsystems of sequences of Higgs lifts
Abstract: Delta-matroids generalize matroids. In a delta-matroid, the counterparts of bases, which are called feasible sets, can have different sizes, but they satisfy a similar exchange property in which symmetric differences replace set differences. One way to get a delta-matroid is to t
From playlist Combinatorics

Matrices in MATLAB | Lecture 7 | Numerical Methods for Engineers
How to construct and operate with matrices in MATLAB. Join me on Coursera: https://www.coursera.org/learn/numerical-methods-engineers Lecture notes at http://www.math.ust.hk/~machas/numerical-methods-for-engineers.pdf Subscribe to my channel: http://www.youtube.com/user/jchasnov?sub_con
From playlist Numerical Methods for Engineers

Zoltán Szigeti: Packing of arborescences with matroid constraints via matroid intersection
The lecture was held within the framework of the follow-up workshop to the Hausdorff Trimester Program: Combinatorial Optimization. Abstract: Edmonds characterized digraphs having a packing of k spanning arborescences in terms of connectivity and later in terms of matroid intersection. D
From playlist Follow-Up-Workshop "Combinatorial Optimization"

Gyula Pap: Linear matroid matching in the oracle model
Gyula Pap: Linear matroid matching in the oracle model Linear matroid matching is understood as a special case of matroid matching when the matroid is given with a matrix representation. However, for certain examples of linear matroids, the matrix representation is not given, and actuall
From playlist HIM Lectures 2015
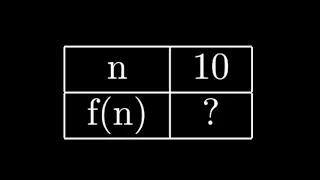
How Many Matroids of Size 10? - #MegaFavNumbers
A matroid is a generalisation of the idea of independence. How many matroids are there on 10 things? A video for #MegaFavNumbers. References: https://www.math.lsu.edu/~oxley/survey4.pdf https://oeis.org/A055545 https://bit.ly/3jzqIwt
From playlist MegaFavNumbers

Connecting tropical intersection theory with polytope algebra in types A and B by Alex Fink
PROGRAM COMBINATORIAL ALGEBRAIC GEOMETRY: TROPICAL AND REAL (HYBRID) ORGANIZERS Arvind Ayyer (IISc, India), Madhusudan Manjunath (IITB, India) and Pranav Pandit (ICTS-TIFR, India) DATE & TIME: 27 June 2022 to 08 July 2022 VENUE: Madhava Lecture Hall and Online Algebraic geometry is t
From playlist Combinatorial Algebraic Geometry: Tropical and Real (HYBRID)

Rico Zenklusen: The Submodular Secretary Problem Goes Linear
During the last decade, the matroid secretary problem (MSP) became one of the most prominent classes of online selection problems. The strong interest in MSPs is due to both its many applications and the fact that matroid constraints have useful properties for the design of strong online a
From playlist HIM Lectures 2015

András Frank: Non TDI Optimization with Supermodular Functions
The notion of total dual integrality proved decisive in combinatorial optimization since it properly captured a phenomenon behind the tractability of weighted optimization problems. For example, we are able to solve not only the maximum cardinality matching (degree-constrained subdigraph,
From playlist HIM Lectures 2015

Lesson 5.5: Variable Number of Arguments
A video segment from the Coursera MOOC on introductory computer programming with MATLAB by Vanderbilt. Lead instructor: Mike Fitzpatrick. Check out the companion website and textbook: http://cs103.net
From playlist Vanderbilt: Introduction to Computer Programming with MATLAB (CosmoLearning Computer Programming)
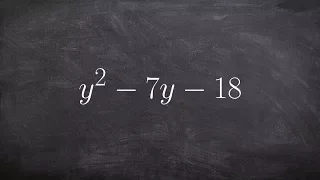
Learn how to factor a trinomial using the diamond method
👉Learn how to factor quadratics. A quadratic is an algebraic expression having two as the highest power of its variable(s). To factor an algebraic expression means to break it up into expressions that can be multiplied together to get the original expression. To factor a quadratic with th
From playlist Factor Quadratic Expressions
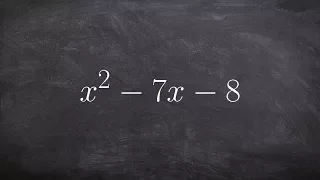
Learning how to factor a quadratic using the box method
👉Learn how to factor quadratics. A quadratic is an algebraic expression having two as the highest power of its variable(s). To factor an algebraic expression means to break it up into expressions that can be multiplied together to get the original expression. To factor a quadratic with th
From playlist Factor Quadratic Expressions
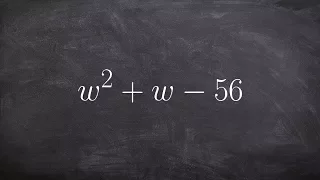
Factoring a trinomial using the diamond method
👉Learn how to factor quadratics. A quadratic is an algebraic expression having two as the highest power of its variable(s). To factor an algebraic expression means to break it up into expressions that can be multiplied together to get the original expression. To factor a quadratic with th
From playlist Factor Quadratic Expressions

Nonlinear algebra, Lecture 13: "Polytopes and Matroids ", by Mateusz Michalek
This is the thirteenth lecture in the IMPRS Ringvorlesung, the advanced graduate course at the Max Planck Institute for Mathematics in the Sciences.
From playlist IMPRS Ringvorlesung - Introduction to Nonlinear Algebra

Victor Chepoi: Simple connectivity, local to global, and matroids
Victor Chepoi: Simple connectivity, local-to-global, and matroids A basis graph of a matroid M is the graph G(M) having the bases of M as the vertex-set and the pairs of bases differing by an elementary exchange as edges. Basis graphs of matroids have been characterized by S.B. Maurer, J.
From playlist HIM Lectures 2015

How to factor a quadratic in your head when a=1
👉Learn how to factor quadratics. A quadratic is an algebraic expression having two as the highest power of its variable(s). To factor an algebraic expression means to break it up into expressions that can be multiplied together to get the original expression. To factor a quadratic with th
From playlist Factor Quadratic Expressions

Anna De Mier: Approximating clutters with matroids
Abstract: There are several clutters (antichains of sets) that can be associated with a matroid, as the clutter of circuits, the clutter of bases or the clutter of hyperplanes. We study the following question: given an arbitrary clutter Λ, which are the matroidal clutters that are closest
From playlist Combinatorics