Variational Monte Carlo

Mathematical optimization | Quantum Monte Carlo

In computational physics, variational Monte Carlo (VMC) is a quantum Monte Carlo method that applies the variational method to approximate the ground state of a quantum system. The basic building block is a generic wave function depending on some parameters . The optimal values of the parameters is then found upon minimizing the total energy of the system. In particular, given the Hamiltonian , and denoting with a many-body configuration, the expectation value of the energy can be written as: Following the Monte Carlo method for evaluating integrals, we can interpret as a probability distribution function, sample it, and evaluate the energy expectation value as the average of the so-called local energy . Once is known for a given set of variational parameters , then optimization is performed in order to minimize the energy and obtain the best possible representation of the ground-state wave-function. VMC is no different from any other variational method, except that the many-dimensional integrals are evaluated numerically. Monte Carlo integration is particularly crucial in this problem since the dimension of the many-body Hilbert space, comprising all the possible values of the configurations , typically grows exponentially with the size of the physical system. Other approaches to the numerical evaluation of the energy expectation values would therefore, in general, limit applications to much smaller systems than those analyzable thanks to the Monte Carlo approach. The accuracy of the method then largely depends on the choice of the variational state. The simplest choice typically corresponds to a mean-field form, where the state is written as a factorization over the Hilbert space. This particularly simple form is typically not very accurate since it neglects many-body effects. One of the largest gains in accuracy over writing the wave function separably comes from the introduction of the so-called Jastrow factor. In this case the wave function is written as , where is the distance between a pair of quantum particles and is a variational function to be determined. With this factor, we can explicitly account for particle-particle correlation, but the many-body integral becomes unseparable, so Monte Carlo is the only way to evaluate it efficiently. In chemical systems, slightly more sophisticated versions of this factor can obtain 80–90% of the correlation energy (see electronic correlation) with less than 30 parameters. In comparison, a configuration interaction calculation may require around 50,000 parameters to reach that accuracy, although it depends greatly on the particular case being considered. In addition, VMC usually scales as a small power of the number of particles in the simulation, usually something like N2−4 for calculation of the energy expectation value, depending on the form of the wave function. (Wikipedia).

Introduction to Direct Variation, Inverse Variation, and Joint Variation

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Introduction to Direct Variation, Inverse Variation, and Joint Variation

From playlist 3.7 Modeling Using Variation

Variation of parameters

Free ebook http://tinyurl.com/EngMathYT I show how to solve differential equations by applying the method of variation of parameters for those wanting to review their understanding.

From playlist Differential equations

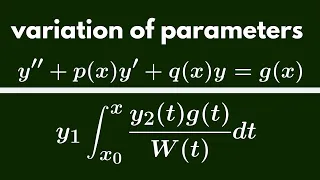
Differential Equations | Variation of Parameters.

We derive the general form for a solution to a differential equation using variation of parameters. http://www.michael-penn.net

From playlist Differential Equations

Statistics - How to calculate the coefficient of variation

In this video I'll quickly show you how to find the coefficient of variation. There are two formulas for samples and populations, but these are basically the same and involve dividing the standard deviation by the mean and lastly converting to a percent. The coefficient of variation is u

From playlist Statistics

Variation of Parameters for Systems of Differential Equations

This is the second part of the variation of parameters-extravaganza! In this video, I show you how to use the same method in the last video to solve inhomogeneous systems of differential equations. Witness how linear algebra makes this method so elegant!

From playlist Differential equations

Derive the Variation of Parameters Formula to Solve Linear Second Order Nonhomogeneous DEs

This video derives or proves the variation of parameters formula used to find a particular solution and solve linear second order nonhomogeneous differential equations. Site: http://mathispower4u.com

From playlist Linear Second Order Nonhomogeneous Differential Equations: Variation of Parameters

Calculus of Variations ft. Flammable Maths

Flammable Maths: https://www.youtube.com/channel/UCtAIs1VCQrymlAnw3mGonhw Leibnitz Rule: https://www.youtube.com/watch?v=wkh1Y7R1sOw This video is an introduction to the calculus of variations. We go over what variational calculus is trying to solve, and derive the Euler-Lagrange equatio

From playlist Analysis

Ex 1: General Solution to a Second Order DE Using Variation of Parameters

This video provides an example of how to determine the general solution to a linear second order nonhomogeneous differential equation. Site: http://mathispower4u.com

From playlist Linear Second Order Nonhomogeneous Differential Equations: Variation of Parameters

Pre-Calculus - Types of variation

In this video I'll introduce the basic types of variation like direct, inverse, and joint variation. Near the end I'll also talk about combined variation where we put these basic forms together. Remember to see how the variable are connected for a clue on the type of variation. For more

From playlist Pre-Calculus

David Ceperley - Introduction to Classical and Quantum Monte Carlo methods for Many-Body systems

Recorded 09 March 2022. David Ceperley of the University of Illinois at Urbana-Champaign presents "Introduction to Classical and Quantum Monte Carlo methods for Many-Body systems" at IPAM's Advancing Quantum Mechanics with Mathematics and Statistics Tutorials. Abstract: Metropolis (Markov

From playlist Tutorials: Advancing Quantum Mechanics with Mathematics and Statistics - March 8-11, 2022

Gunther Leobacher: Quasi Monte Carlo Methods and their Applications

In the first part, we briefly recall the theory of stochastic differential equations (SDEs) and present Maruyama's classical theorem on strong convergence of the Euler-Maruyama method, for which both drift and diffusion coefficient of the SDE need to be Lipschitz continuous. VIRTUAL LECTU

From playlist Virtual Conference

Robert Tichy: Quasi-Monte Carlo methods and applications: introduction

VIRTUAL LECTURE Recording during the meeting "Quasi-Monte Carlo Methods and Applications " the October 28, 2020 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematician

From playlist Virtual Conference

Rémy Leluc

From playlist Contributed talks One World Symposium 2020

HEDS | Solving the Many-Electron Schrödinger Equation with Deep Neural Network

HEDS Seminar Series- Matthew Foulkes – February 4th, 2021 LLNL-VIDEO- 825208

From playlist High Energy Density Science Seminar Series

HEDS | Solving the Many-Electron Schrödinger Equation with Deep Neural Networks

Seminar Series talk by Matthew Foulkes, Feb. 4, 2021. LLNL-VIDEO- 825208

From playlist High Energy Density Science Seminar Series

Giray Ökten: Number sequences for simulation - lecture 2

After an overview of some approaches to define random sequences, we will discuss pseudorandom sequences and low-discrepancy sequences. Applications to numerical integration, Koksma-Hlawka inequality, and Niederreiter’s uniform point sets will be discussed. We will then present randomized q

From playlist Probability and Statistics

Stanford CS229: Machine Learning | Summer 2019 | Lecture 20 - Variational Autoencoder

For more information about Stanford’s Artificial Intelligence professional and graduate programs, visit: https://stanford.io/ai Anand Avati Computer Science, PhD To follow along with the course schedule and syllabus, visit: http://cs229.stanford.edu/syllabus-summer2019.html

From playlist Stanford CS229: Machine Learning Course | Summer 2019 (Anand Avati)

Working with Parameter Uncertainty | Robust Control, Part 4

Watch the first videos in this series: Robust Control, Part 1: What Is Robust Control? - https://youtu.be/A7wHSr6GRnc Robust Control, Part 2: Understanding Disk Margin - https://youtu.be/XazdN6eZF80 Robust Control, Part 3: Disk Margins for MIMO Systems - https://youtu.be/sac_IYBjcq0 The

From playlist Robust Control

PauliNet - Deep neural network solution of the electronic Schrödinger equation

Paper: https://arxiv.org/abs/1909.08423 Code: https://github.com/deepqmc/deepqmc

From playlist Research

Variation of parameters to solve differential equations

Free ebook http://tinyurl.com/EngMathYT How to use the method of variation of parameters to solve second order ordinary differential equations with constant coefficients. Several examples are discussed.

From playlist Differential equations

Variational Monte Carlo

Related pages