Van Aubel's theorem
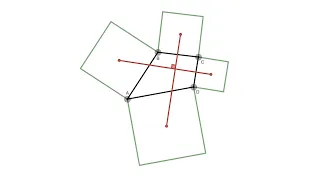
In plane geometry, Van Aubel's theorem describes a relationship between squares constructed on the sides of a quadrilateral. Starting with a given convex quadrilateral, construct a square, external to the quadrilateral, on each side. Van Aubel's theorem states that the two line segments between the centers of opposite squares are of equal lengths and are at right angles to one another. Another way of saying the same thing is that the center points of the four squares form the vertices of an equidiagonal orthodiagonal quadrilateral. The theorem is named after Belgian mathematician Henricus Hubertus (Henri) Van Aubel (1830–1906), who published it in 1878. The theorem holds true also for re-entrant quadrilaterals, and when the squares are constructed internally to the given quadrilateral. For complex (self-intersecting) quadrilaterals, the external and internal constructions for the squares are not definable. In this case, the theorem holds true when the constructions are carried out in the more general way: * follow the quadrilateral vertices in a sequential direction and construct each square on the right hand side of each side of the given quadrilateral. * Follow the quadrilateral vertices in the same sequential direction and construct each square on the left hand side of each side of the given quadrilateral. The segments joining the centers of the squares constructed externally (or internally) to the quadrilateral over two opposite sides have been referred to as Van Aubel segments. The points of intersection of two equal and orthogonal Van Aubel segments (produced when necessary) have been referred to as Van Aubel points: first or outer Van Aubel point for the external construction, second or inner Van Aubel point for the internal one. The Van Aubel theorem configuration presents some relevant features, among others: * the Van Aubel points are the centers of the two circumscribed squares of the quadrilateral. * The Van Aubel points, the mid-points of the quadrilateral diagonals and the mid-points of the Van Aubel segments are concyclic. A few extensions of the theorem, considering similar rectangles, similar rhombi and similar parallelograms constructed on the sides of the given quadrilateral, have been published on The Mathematical Gazette. (Wikipedia).